
【题目】如图,已知△ABP是等腰三角形,AB=BP,以AB为直径的⊙O交AP于点D,交BP于点C,连接BD交AC于点G,直线MN过点A,且∠PAM= ![]() ∠ABP.
∠ABP.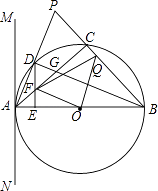
(1)试说明直线MN是⊙O的切线.
(2)过D作DE⊥AB于E,交AC于F,求证:△DFG是等腰三角形.
(3)连结FO,过点O作OQ⊥FO交BP于点Q,连结FQ,求证:FQ2=AF2+BQ2 .
【答案】
(1)
解:∵AB为直径,
∴∠ADB=90°,
∴BD⊥AP,
∵BA=BP,
∴BD平分∠ABP,即∠ABD= ![]() ∠ABP,
∠ABP,
∵∠PAM= ![]() ∠ABP,
∠ABP,
∴∠PAM=∠ABD,
∵∠ABD+∠BAD=90°,
∴∠PAM+∠BAD=90°,即∠BAM=90°,
∴AB⊥MN,
∴直线MN是⊙O的切线;
(2)
证明:∵DE⊥AB,
∴∠BDE+∠DBE=90°,
而∠DBA+∠DAB=90°,
∴∠BDE=∠DAE,
∵∠AGD=∠GBA+∠GAB
而∠GBA=∠DBC=∠DAC,
∴∠AGD=∠DAC+∠GAB=∠DAE,
∴∠BDE=∠AGD,
∴△DFG是等腰三角形;
(3)
延长QO到点K,使OK=OQ,如图,

∵OQ⊥OF,OQ=OK,即FO垂直平分QK,
∴FK=FQ,
在△OBQ和△OAK中,
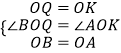 ,
,
∴△OBQ≌△OAK,
∴BQ=AK,∠OBQ=∠OAK,
∵AB为直径,
∴∠ACB=90°,
∴∠CAB+∠ABC=90°,
∴∠CAB+∠OAK=90°,即∠FAK=90°,
在Rt△AFK中,FK2=AF2+AK2,
∴FQ2=AF2+BQ2.
【解析】(1)根据圆周角定理得到∠ADB=90°,而BA=BP,根据等腰三角形的性质得∠ABD= ![]() ∠ABP,加上∠PAM=
∠ABP,加上∠PAM= ![]() ∠ABP,所以∠PAM=∠ABD,则利用∠ABD+∠BAD=90°可得∠PAM+∠BAD=90°,于是根据切线的判定定理可得直线MN是⊙O的切线;(2)先利用等角的余角相等得到∠BDE=∠DAE,再利用三角形外角性质得∠AGD=∠GBA+∠GAB,然后利用等量代换可得∠AGD=∠DAC+∠GAB=∠DAE,于是有∠BDE=∠AGD,根据等腰三角形的判定即可得到△DFG是等腰三角形;(3)延长QO到点K,使OK=OQ,如图,先证明FO垂直平分QK得到FK=FQ,再证明△OBQ≌△OAK得到BQ=AK,∠OBQ=∠OAK,接着根据圆周角定理得到∠ACB=90°,即∠CAB+∠ABC=90°,易得∠CAB+∠OAK=90°,即∠FAK=90°,然后在Rt△AFK中,根据勾股定理得到FK2=AF2+AK2 , 再利用等线段代换即可得到结论.
∠ABP,所以∠PAM=∠ABD,则利用∠ABD+∠BAD=90°可得∠PAM+∠BAD=90°,于是根据切线的判定定理可得直线MN是⊙O的切线;(2)先利用等角的余角相等得到∠BDE=∠DAE,再利用三角形外角性质得∠AGD=∠GBA+∠GAB,然后利用等量代换可得∠AGD=∠DAC+∠GAB=∠DAE,于是有∠BDE=∠AGD,根据等腰三角形的判定即可得到△DFG是等腰三角形;(3)延长QO到点K,使OK=OQ,如图,先证明FO垂直平分QK得到FK=FQ,再证明△OBQ≌△OAK得到BQ=AK,∠OBQ=∠OAK,接着根据圆周角定理得到∠ACB=90°,即∠CAB+∠ABC=90°,易得∠CAB+∠OAK=90°,即∠FAK=90°,然后在Rt△AFK中,根据勾股定理得到FK2=AF2+AK2 , 再利用等线段代换即可得到结论.


科目:初中数学 来源: 题型:
【题目】(本题满分10分为迎接建党90周年,某校组织了以“党在我心中”为主题的电子小报制作比赛,评分结果只有60,70,80,90,100五种.现从中随机抽取部分作品,对其份数及成绩进行整理,制成如下两幅不完整的统计图.

根据以上信息,解答下列问题:
(1)求本次抽取了多少份作品,并补全两幅统计图;
(2)已知该校收到参赛作品共900份,请估计该校学生比赛成绩达到90分以上(含90分)的作品有多少份?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.
(1)求AD的长及抛物线的解析式;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动,设运动时间为t秒,当t为何值时,以P,Q,C为顶点的三角形与ADE相似?
(3)点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M,N,C,E为顶点的四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了纪念中国共产主义青年团成立90周年,某校初三(1)、(2)班团支部组织了一次联欢会,小乐为活动设计了一个游戏:把两个可以自由转动的转盘各等分成三个扇形,分别标上1,2,3和4,5,6,每班级各派一名选手参加,每人同时转动两个转盘各一次(指针落在等分线上重转),转盘停止后,指针指向的数字之和为偶数时(1)班获胜,数字之和为奇数时(2)班获胜,小乐设计的游戏规则公平吗?请用树状图或列表分析说明,若认为不公平,请修改规则使游戏变得公平.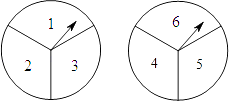
查看答案和解析>>
科目:初中数学 来源: 题型:
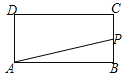
【题目】如图,在长方形ABCD中,AB=2,BC=1,运点P从点B出发,沿路线B![]() C
C![]() D作匀速运动,那么△ABP的面积
D作匀速运动,那么△ABP的面积![]() 与点P运动的路程之间的函数图象大致是( ).
与点P运动的路程之间的函数图象大致是( ).
A. 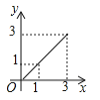 B.
B. 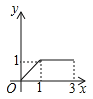 C.
C. 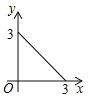 D.
D. 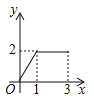
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣ ![]() x+3与坐标轴交于A,B两点,设P,Q分别为AB边,OB边上的动点,它们同时分别从点A,点O以每秒1个单位速度向终点B匀速移动,当一个点到达终点时另一个点也停止移动,设移动时间为t秒.
x+3与坐标轴交于A,B两点,设P,Q分别为AB边,OB边上的动点,它们同时分别从点A,点O以每秒1个单位速度向终点B匀速移动,当一个点到达终点时另一个点也停止移动,设移动时间为t秒.
(1)请写出点A,点B的坐标;
(2)试求△OPQ的面积S与移动时间t之间的函数关系式,当t为何值时,S有最大值?并求出S的最大值;
(3)试证明无论t为何值,△OPQ都不会是等边三角形;
(4)将△OPQ沿直线PQ折叠,得到△O′PQ,问:△OPQ和O′PQ能否拼成一个三角形?若能,求出点O′的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的周长为6π,半径是1的⊙O从与AB相切于点D的位置出发,在△ABC外部按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,则⊙O自转了( ) 
A.2周
B.3周
C.4周
D.5周
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某生物兴趣小组在四天的试验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同.他们将一头骆驼前两昼夜的体温变化情况绘制成如图所示的图象,请根据图象完成下列问题:
(1)第一天中,在什么时间范围内这头骆驼的体温是上升的?它的体温从最低上升到最高需要多长时间?
(2)第三天12时这头骆驼的体温是多少?
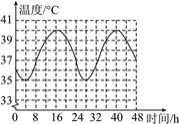
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,动点P从点A出发,以3个单位/秒的速度沿着数轴负方向匀速运动,设运动时间为t秒(t>0).
![]()
(1)写出数轴上点B表示的数 ;动点P对应的数是 (用含t的代数式表示);
(2)动点Q从点B出发,以1个单位/秒的速度匀速运动,且点P, Q同时出发
①若动点Q沿着数轴正方向匀速运动,多少秒时点P与点Q相遇?
②若动点Q沿着数轴负方向匀速运动,多少秒时点P与点Q相距4个单位?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com