[题目]如果等腰三角形的一边长为8.另一边长为10.那么连结这个三角形各边的中点所成的三角形的周长为 . 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如果等腰三角形的一边长为8，另一边长为10，那么连结这个三角形各边的中点所成的三角形的周长为 _______.

【答案】13或14

【解析】

作图分析，根据中位线定理得出△DEF的周长等于△ABC的周长的一半，再分两种情况讨论，从而求得其周长．

解：如图，△ABC中，AB=AC=8cm，BC=10cm，D、E、F分别是边AB、BC、AC的中点．

求△DEF的周长．
①∵AB=AC=8，BC=10，D、E、F分别是边AB、BC、AC的中点，
∴DE=BC，DF=AC，EF=AB，
∴△DEF的周长=DE+DF+EF=（8+8+10）=13，

②∵AB=AC=10，BC=8，D、E、F分别是边AB、BC、AC的中点，
∴DE=BC，DF=AC，EF=AB，
∴△DEF的周长=DE+DF+EF=（8+10+10）=14，
故答案为：13或14．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】已知二次函数y=ax2+bx﹣3a经过点A（﹣1，0）、C（0，3），与x轴交于另一点B，抛物线的顶点为D．

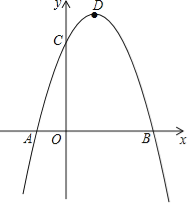
（1）求此二次函数解析式；

（2）连接DC、BC、DB，求证：△BCD是直角三角形；

（3）在对称轴右侧的抛物线上是否存在点P，使得△PDC为等腰三角形？若存在，求出符合条件的点P的坐标；若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】（12分）如图1，点O是正方形ABCD两对角线的交点，分别延长OD到点G，OC到点E，使OG=2OD，OE=2OC，然后以OG、OE为邻边作正方形OEFG，连接AG，DE．

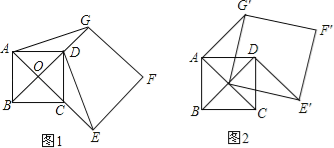
（1）求证：DE⊥AG；

（2）正方形ABCD固定，将正方形OEFG绕点O逆时针旋转α角（0°＜α＜360°）得到正方形OE′F′G′，如图2．

①在旋转过程中，当∠OAG′是直角时，求α的度数；

②若正方形ABCD的边长为1，在旋转过程中，求AF′长的最大值和此时α的度数，直接写出结果不必说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，已知抛物线经过，两点，与x轴的另一个交点为C，顶点为D，连结CD．

（1）求该抛物线的表达式；

（2）点P为该抛物线上一动点（与点B、C不重合），设点P的横坐标为t．

①当点P在直线BC的下方运动时，求的面积的最大值；

②该抛物线上是否存在点P，使得若存在，求出所有点P的坐标；若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】（题文）如图，在等腰直角三角形MNC中，CN＝MN＝，将△MNC绕点C顺时针旋转60°，得到△ABC，连接AM，BM，BM交AC于点O.

(1)∠NCO的度数为________；

(2)求证：△CAM为等边三角形；

(3)连接AN，求线段AN的长．

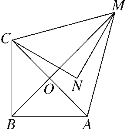
查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】

情境观察：将矩形ABCD纸片沿对角线AC剪开，得到△ABC和△A′C′D，如图1所示.将△A′C′D的顶点A′与点A重合，并绕点A按逆时针方向旋转，使点D、A(A′)、B在同一条直线上，如图2所示．

观察图2可知：与BC相等的线段是 ▲ ，∠CAC′= ▲ °．

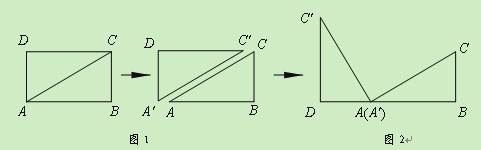
问题探究：如图3，△ABC中，AG⊥BC于点G，以A为直角顶点，分别以AB、AC为直角边，向△ABC外作等腰Rt△ABE和等腰Rt△ACF，过点E、F作射线GA的垂线，垂足分别为P、Q. 试探究EP与FQ之间的数量关系，并证明你的结论.

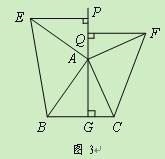
拓展延伸：如图4，△ABC中，AG⊥BC于点G，分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF，射线GA交EF于点H. 若AB=k AE，AC=k AF，试探究HE与HF之间的数量关系，并说明理由.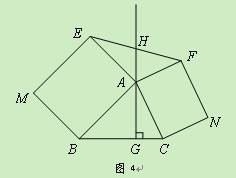

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，线段AC＝n+1（其中n为正整数），点B在线段AC上，在线段AC同侧作菱形ABMN与菱形BCEF，点F在BM边上，AB＝n，∠ABM＝60°，连接AM、ME、EA得到△AME．当AB＝1时，△AME的面积记为S1；当AB＝2时，△AME的面积记为S2；当AB＝3时，△AME的面积记为S3；…；当AB＝n时，△AME的面积记为Sn，当n≥2时，Sn﹣Sn﹣1＝__．