
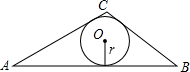
 已知任意三角形的三边长,如何求三角形面积?
已知任意三角形的三边长,如何求三角形面积?分析 (1)先根据BC、AC、AB的长求出P,再代入到公式S=$\sqrt{p(p-a)(p-b)(p-c)}$即可求得S的值;
(2)根据公式S=$\frac{1}{2}$r(AC+BC+AB),代入可得关于r的方程,解方程得r的值.
解答 解:(1)∵BC=5,AC=6,AB=9,
∴p=$\frac{BC+AC+AB}{2}$=$\frac{5+6+9}{2}$=10,
∴S=$\sqrt{p(p-a)(p-b)(p-c)}$=$\sqrt{10×5×4×1}$=10$\sqrt{2}$;
故△ABC的面积10$\sqrt{2}$;
(2)∵S=$\frac{1}{2}$r(AC+BC+AB),
∴10$\sqrt{2}$=$\frac{1}{2}$r(5+6+9),
解得:r=$\sqrt{2}$,
故△ABC的内切圆半径r=$\sqrt{2}$.
点评 本题主要三角形的内切圆与内心、二次根式的应用,熟练掌握三角形的面积与内切圆半径间的公式是解题的关键.


科目:初中数学 来源: 题型:填空题
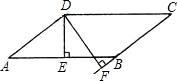 如图所示,?ABCD的周长是10$\sqrt{3}$+6$\sqrt{2}$,AB的长是5$\sqrt{3}$,DE⊥AB于E,DF⊥CB交CB的延长线于点F,DE的长是3,则DF的长为$\frac{5\sqrt{6}}{2}$.
如图所示,?ABCD的周长是10$\sqrt{3}$+6$\sqrt{2}$,AB的长是5$\sqrt{3}$,DE⊥AB于E,DF⊥CB交CB的延长线于点F,DE的长是3,则DF的长为$\frac{5\sqrt{6}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
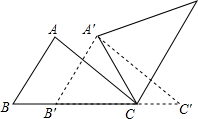 如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离为2,旋转角的度数为60°.
如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离为2,旋转角的度数为60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
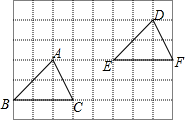 如图,△ABC经过怎样的平移得到△DEF( )
如图,△ABC经过怎样的平移得到△DEF( )| A. | 把△ABC向左平移5个单位,再向下平移2个单位 | |
| B. | 把△ABC向右平移5个单位,再向下平移2个单位 | |
| C. | 把△ABC向右平移5个单位,再向上平移2个单位 | |
| D. | 把△ABC向左平移5个单位,再向上平移两个单位 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平行四边形的对角线互相平分 | B. | 等腰梯形的对角线相等 | ||
| C. | 对角线互相垂直的四边形是菱形 | D. | 对角线相等的菱形是正方形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com