
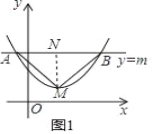
【题目】如图,抛物线y=ax2+bx+c(a>0)的顶点为M,直线y=m与抛物线交于点A,B,若△AMB为等腰直角三角形,我们把抛物线上A,B两点之间的部分与线段AB 围成的图形称为该抛物线对应的准蝶形,线段AB称为碟宽,顶点M 称为碟顶.

(1)由定义知,取AB中点N,连结MN,MN与AB的关系是_____.
(2)抛物线y=![]() 对应的准蝶形必经过B(m,m),则m=_____,对应的碟宽AB是_____.
对应的准蝶形必经过B(m,m),则m=_____,对应的碟宽AB是_____.
(3)抛物线y=ax2﹣4a﹣![]() (a>0)对应的碟宽在x 轴上,且AB=6.
(a>0)对应的碟宽在x 轴上,且AB=6.
①求抛物线的解析式;
②在此抛物线的对称轴上是否有这样的点P(xp,yp),使得∠APB为锐角,若有,请求出yp的取值范围.若没有,请说明理由.
【答案】(1)MN与AB的关系是:MN⊥AB,MN=![]() AB,(2)2,4;(3)①y=
AB,(2)2,4;(3)①y=![]() x2﹣3;②在此抛物线的对称轴上有这样的点P,使得∠APB 为锐角,yp的取值范围是yp<﹣3或yp>3.
x2﹣3;②在此抛物线的对称轴上有这样的点P,使得∠APB 为锐角,yp的取值范围是yp<﹣3或yp>3.
【解析】
(1)直接利用等腰直角三角形的性质分析得出答案;
(2)利用已知点为B(m,m),代入抛物线解析式进而得出m的值,即可得出AB的值;
(3)①根据题意得出抛物线必过(3,0),进而代入求出答案;
②根据y=![]() x2﹣3的对称轴上P(0,3),P(0,﹣3)时,∠APB 为直角,进而得出答案.
x2﹣3的对称轴上P(0,3),P(0,﹣3)时,∠APB 为直角,进而得出答案.
(1)MN与AB的关系是:MN⊥AB,MN=![]() AB,
AB,
如图1,∵△AMB是等腰直角三角形,且N为AB的中点,
∴MN⊥AB,MN=![]() AB,
AB,
故答案为:MN⊥AB,MN=![]() AB;
AB;
(2)∵抛物线y=![]() 对应的准蝶形必经过B(m,m),
对应的准蝶形必经过B(m,m),
∴m=![]() m2,
m2,
解得:m=2或m=0(不合题意舍去),
当m=2则,2=![]() x2,
x2,
解得:x=±2,
则AB=2+2=4;
故答案为:2,4;
(3)①由已知,抛物线对称轴为:y轴,
∵抛物线y=ax2﹣4a﹣![]() (a>0)对应的碟宽在x 轴上,且AB=6.
(a>0)对应的碟宽在x 轴上,且AB=6.
∴抛物线必过(3,0),代入y=ax2﹣4a﹣![]() (a>0),
(a>0),
得,9a﹣4a﹣![]() =0,
=0,
解得:a=![]() ,
,
∴抛物线的解析式是:y=![]() x2﹣3;
x2﹣3;
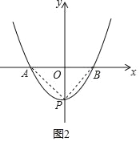
②由①知,如图2,y=![]() x2﹣3的对称轴上P(0,3),P(0,﹣3)时,∠APB 为直角,
x2﹣3的对称轴上P(0,3),P(0,﹣3)时,∠APB 为直角,
∴在此抛物线的对称轴上有这样的点P,使得∠APB 为锐角,yp的取值范围是yp<﹣3或yp>3.


科目:初中数学 来源: 题型:
【题目】4张相同的卡片分别写有数字﹣1、﹣3、4、6,将这些卡片的背面朝上,并洗匀.
(1)从中任意抽取1张,抽到的数字大于0的概率是______;
(2)从中任意抽取1张,并将卡片上的数字记作二次函数y=ax2+bx中的a,再从余下的卡片中任意抽取1张,并将卡片上的数字记作二次函数y=ax2+bx中的b,利用树状图或表格的方法,求出这个二次函数图象的对称轴在y轴右侧的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点A,B,C.现有下面四个推断:①抛物线开口向下;②当x=-2时,y取最大值;③当m<4时,关于x的一元二次方程ax2+bx+c=m必有两个不相等的实数根;④直线y=kx+c(k≠0)经过点A,C,当kx+c> ax2+bx+c时,x的取值范围是-4<x<0;其中推断正确的是 ( )
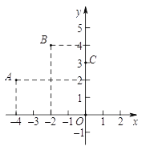
A. ①②B. ①③C. ①③④D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年下半年以来,猪肉价格不断上涨,主要是由非洲猪瘟疫情导致.非洲猪瘟疫情发病急,蔓延速度快.某养猪场第一天发现3头生猪发病,两天后发现共有192头生猪发病.
(1)求每头发病生猪平均每天传染多少头生猪?
(2)若疫情得不到有效控制,按照这样的传染速度,3天后生猪发病头数会超过1500头吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)【问题发现】
如图1,在Rt△ABC中,AB=AC=2,∠BAC=90°,点D为BC的中点,以CD为一边作正方形CDEF,点E恰好与点A重合,则线段BE与AF的数量关系为
(2)【拓展研究】
在(1)的条件下,如果正方形CDEF绕点C旋转,连接BE,CE,AF,线段BE与AF的数量关系有无变化?请仅就图2的情形给出证明;
(3)【问题发现】
当正方形CDEF旋转到B,E,F三点共线时候,直接写出线段AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
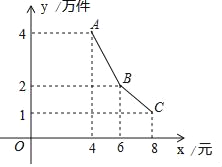
【题目】为了支持大学生创业,某市政府出台了一项优惠政策:提供10万元的无息创业贷款.小王利用这笔贷款,注册了一家淘宝网店,招收5名员工,销售一种火爆的电子产品,并约定用该网店经营的利润,逐月偿还这笔无息贷款.已知该产品的成本为每件4元,员工每人每月的工资为4千元,该网店还需每月支付其它费用1万元.该产品每月销售量y(万件)与销售单价x(元)万件之间的函数关系如图所示.
(1)求该网店每月利润w(万元)与销售单价x(元)之间的函数表达式;
(2)小王自网店开业起,最快在第几个月可还清10万元的无息贷款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市大力发展乡村旅游产业,全力打造客都美丽乡村”,其中“客家美景、客家文化、客家美食”享誉全省,游人络绎不绝.去年我市某村村民抓住机遇,投入20万元创办农家乐(餐饮+住宿),一年时间就收回投资的80%,其中餐饮收入是住宿收入的2倍还多1万元.
(1)求去年该农家乐餐饮和住宿的收入各为多少万元?
(2)今年该村村民再投入了10万元,增设了土特产的实体销售和网上销售项目并实现盈利,村民在接受记者采访时说,预计今年餐饮和住宿的收入比去年还会有10%的增长.这两年的总收入除去所有投资外还能获得不少于10万元的纯利润,请问今年土特产销售至少收入多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com