
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
乘法公式的探究及应用
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,面积是 (写成多项式乘法的形式);

(3)比较图1、图2阴影部分的面积,可以得到公式 ;
(4)运用你所得到的公式,计算:(a+b-2c)(a-b+2c).
查看答案和解析>>
科目:初中数学 来源: 题型:
随着北京的城市扩张、工业发展和人口膨胀,丰富的地表水系迅速断流、干涸,甚至地下水也超采严重,缺水非常严重. 为了解决水资源紧缺问题,市政府采取了一系列措施. 2014年4月16日北京市发改委公布了两套北京水价调整听证方案,征求民意.
方案一
第1阶梯:户年用水量不超145立方米,每立方米水价为4.95元
第2阶梯:户年用水量为146-260立方米,每立方米水价为7元
第3阶梯:户年用水量为260立方米以上,每立方米水价为9元
方案二
第1阶梯:户年用水量不超180立方米,每立方米水价为5元
第2阶梯:户年用水量为181-260立方米,每立方米水价为7元
第3阶梯:户年用水量为260立方米以上,每立方米水价为9元
例如,若采用方案一,当户年用水量为180立方米时,水费为 .
.
请根据方案一、二解决以下问题:
(1) 若采用方案二,当户年水费1040元时,用水量为多少立方米?
(2) 根据本市居民家庭用水情况调查分析,有93%的居民家庭年用水量在第一阶梯.
因此我们以户年用水量180立方米为界,即当户年用水量不超过180立方米时,选择哪个方案所缴纳的水费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
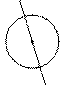
我们把能够平分一个图形面积的直线叫“好线”,如图1.

|
|
|
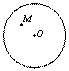
问题情境:如图2,M是圆O内的一定点,请在图2中作出两条“好线”(要求其中一条“好线”必须过点M),使它们将圆O的面积四等分.
小明的思路是:如图3,过点M、O画一条“好线”,过O作OM的垂线,即为另一条“好线”.所以这两条“好线”将的圆O的面积四等分.
问题迁移:(1)请在图4中作出两条“好线”,使它们将□ABCD的面积四等分;
(2)如图5,M是正方形 内一定点,请在图5中作出两条“好线”(要求其中一条“好线”必须过点
内一定点,请在图5中作出两条“好线”(要求其中一条“好线”必须过点 ),使它们将正方形
),使它们将正方形 的面积四等分;
的面积四等分;
|
 中,
中,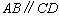 ,
,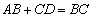 ,点
,点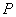 是
是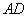 的中点,点
的中点,点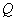 是边
是边 一点,请作出“好线”
一点,请作出“好线”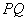 将四边形
将四边形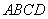 的面积分成相等的两部分.
的面积分成相等的两部分. 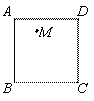
|
| |||
| |||
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( )

A.AB∥DC,AD=BC B. AB∥DC,AD∥BC C. AB=DC,AD=BC D. OA=OC,OB=OD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com