
【题目】已知![]() ,
,![]() ,
,![]() 是
是![]() 边上一点,延长
边上一点,延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 的垂直平分线于点
的垂直平分线于点![]() ,连接
,连接![]() .
.
(1)如图1,当点![]() 与点
与点![]() 重合时,证明:
重合时,证明:![]() ;
;

(2)如图2,当点![]() 不与
不与![]() ,
,![]() 两点重合时,(1)中的结论是否还成立?并说明理由.
两点重合时,(1)中的结论是否还成立?并说明理由.
【答案】(1)见解析(2)成立,理由见解析
【解析】
(1)延长FD至点G,使得DG=DF,连接BG,AG.
先证明△ADG≌△EDF,得到AG=EF.再证明△ABG≌△DBF,得到∠ABG=∠DBF,即有∠ABG=∠DBG=![]() ∠ABC=30°,进而得到∠DBF=30°,根据30°角所对的直角边等于斜边的一半即可得到结论.
∠ABC=30°,进而得到∠DBF=30°,根据30°角所对的直角边等于斜边的一半即可得到结论.
(2)成立.延长FD至点![]() ,使得DG=DF,连接BG,AG.
,使得DG=DF,连接BG,AG.
通过证明△ADG≌△EDF,得到AG=EF.由垂直平分线的性质得到FC=FE,从而有AG=CF.
即可得到△ABG≌△CBF,由全等三角形对应角相等得到∠ABG=∠CBF,即有∠ABG=∠GBD.进而得出∠DBF=∠GBD=30°,根据30°角所对的直角边等于斜边的一半即可得到结论.
延长FD至点G,使得DG=DF,连接BG,AG.
∵DF⊥BC于点![]() ,∴∠BDF=90°,∴BG=BF,∴∠DBF=∠DBG.
,∴∠BDF=90°,∴BG=BF,∴∠DBF=∠DBG.
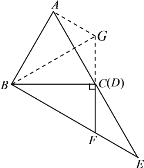
又∵AD=ED,∠ADG=∠EDF,DG=DF,∴△ADG≌△EDF(SAS),∴AG=EF.
∵点![]() 在CE的垂直平分线上,点
在CE的垂直平分线上,点![]() 与点
与点![]() 重合,∴DF=EF,∴DF=AG.
重合,∴DF=EF,∴DF=AG.
∵AB=BC,∴△ABG≌△DBF(SSS),∴∠ABG=∠DBF,∴∠ABG=∠DBG=![]() ∠ABC=30°,∴∠DBF=30°,∴BG=2DG,∴BF=2DF.
∠ABC=30°,∴∠DBF=30°,∴BG=2DG,∴BF=2DF.
(2)成立.理由如下:
延长FD至点![]() ,使得DG=DF,连接BG,AG.
,使得DG=DF,连接BG,AG.
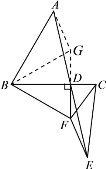
∵DF⊥BC于点![]() ,∴∠BDF=90°,∴BG=BF,∴∠DBF=∠DBG.
,∴∠BDF=90°,∴BG=BF,∴∠DBF=∠DBG.
又∵AD=ED,∠ADG=∠EDF,∴△ADG≌△EDF(SAS),∴AG=EF.
∵点![]() 在CE的垂直平分线上,∴FC=FE,∴AG=CF.
在CE的垂直平分线上,∴FC=FE,∴AG=CF.
又∵AB=BC,∴△ABG≌△CBF(SSS),∴∠ABG=∠CBF,∴∠ABG=∠GBD.
又∵∠ABC=60°,∴∠GBD=30°,∴∠DBF=∠GBD=30°,∴BF=2DF.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′,边BC与D′C′交于点O,则四边形ABOD′的周长是( )

A. 6![]() B. 6C. 3
B. 6C. 3![]() D. 3+3
D. 3+3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=ABAD.我们称该四边形为“可分四边形”,∠DAB称为“可分角”.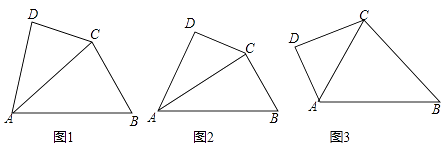
(1)如图2,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(2)如图3,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则求∠DAB的度数;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,则△DAB的最大面积等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是等边三角形ABC中BA延长线上一点,连接CD,E是BC上一点,且DE=DC,若BD+BE=![]() ,CE=
,CE=![]() ,则这个等边三角形的边长是__________.
,则这个等边三角形的边长是__________.
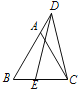
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场11月初花费15 000元购进一批某品牌英语点读笔,因深受顾客喜爱,销售一空.该商场于12月初又花费24 000元购进一批同品牌英语点读笔,且所购数量是11月初的1.5倍,但每支进价涨了10元.
(1)求商场11月初购进英语点读笔多少支?
(2)11月份商场该品牌点读笔每支的售价是270元,若12月份购买的点读笔全部售完,且所获利润是11月份利润的1.2倍,求12月份该品牌点读笔每支的售价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两地被大山阻隔,若要从A地到B地,只能沿着如图所示的公路先从A地到C地,再由C地到B地.现计划开凿隧道A,B两地直线贯通,经测量得:∠CAB=30°,∠CBA=45°,AC=20km,求隧道开通后与隧道开通前相比,从A地到B地的路程将缩短多少?(结果精确到0.1km,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)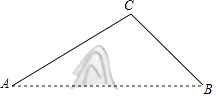
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】码头工人每天往一艘轮船上装载30吨货物,装载完毕恰好用了8天时间.
(1)轮船到达目的地开始卸货,平均卸货速度v(单位:吨/天)与卸货天数t之间有怎样的函数关系?
(2)由于遇到紧急情况,要求船上货物不超过5天卸货完毕,那么平均每天至少要缷货多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=30°,点B1、B2、B3…和A1、A2、A3…分别在OM和ON上,且△A1B1A2、△A2B2A3、△A3B3A4、…分别为等边三角形,已知OA1=1,则△A2018B2018A2019的边长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,B是线段AD上一动点,沿A→D→A以2cm/s的速度往返运动1次,C是线段BD的中点,AD=10cm,设点B运动时间为t秒(0≤t≤10).
(1)当t=2时,①AB= cm.②求线段CD的长度.
(2)①点B沿点A→D运动时,AB= cm;
②点B沿点D→A运动时,AB= cm.(用含t的代数式表示AB的长)
(3)在运动过程中,若AB中点为E,则EC的长是否变化,若不变,求出EC的长;若发生变化,请说明理由.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com