
【题目】抛物线y=ax2+c与x轴交于A,B两点,顶点为C,点P为抛物线上,且位于x轴下方.
(1)如图1,若P(1,﹣3),B(4,0).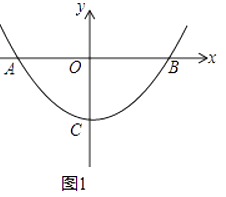
①求该抛物线的解析式;
②若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
(2)如图2,已知直线PA,PB与y轴分别交于E、F两点.当点P运动时, ![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
【答案】
(1)解:①将P(1,﹣3),B(4,0)代入y=ax2+c,得
![]() ,解得
,解得  ,
,
抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() ;
;
②如图1,
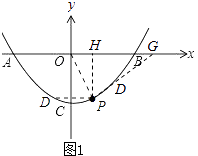
当点D在OP左侧时,
由∠DPO=∠POB,得
DP∥OB,
D与P关于y轴对称,P(1,﹣3),
得D(﹣1,﹣3);
当点D在OP右侧时,延长PD交x轴于点G.
作PH⊥OB于点H,则OH=1,PH=3.
∵∠DPO=∠POB,
∴PG=OG.
设OG=x,则PG=x,HG=x﹣1.
在Rt△PGH中,由x2=(x﹣1)2+32,得x=5.
∴点G(5,0).
∴直线PG的解析式为y= ![]() x﹣
x﹣ ![]()
解方程组 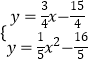 得
得 ![]() ,
,  .
.
∵P(1,﹣3),
∴D( ![]() ,﹣
,﹣ ![]() ).
).
∴点D的坐标为(﹣1,﹣3)或( ![]() ,﹣
,﹣ ![]() )
)
(2)解:点P运动时, ![]() 是定值,定值为2,理由如下:
是定值,定值为2,理由如下:
作PQ⊥AB于Q点,设P(m,am2+c),A(﹣t,0),B(t,0),则at2+c=0,c=﹣at2.
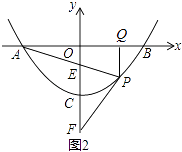
∵PQ∥OF,
∴ ![]() ,
,
∴OF= ![]() =﹣
=﹣ ![]() =
= ![]() =amt+at2.
=amt+at2.
同理OE=﹣amt+at2.
∴OE+OF=2at2=﹣2c=2OC.
∴ ![]() =2.
=2.
【解析】(1)①根据待定系数法求函数解析式,可得答案;②根据平行线的判定,可得PD∥OB,根据函数值相等两点关于对称轴对称,可得D点坐标;(2)根据待定系数法,可得E、F点的坐标,根据分式的性质,可得答案.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】预习了“线段、射线、直线”一节的内容后,乐乐所在的小组,对如图展开了激烈的讨论,下列说法不正确的是( )
![]()
A. 直线AB与直线BA是同一条直线
B. 射线OA与射线AB是同一条射线
C. 射线OA与射线OB是同一条射线
D. 线段AB与线段BA是同一条线段
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年4月20日19点41分,天舟一号由长征七号火箭发生升空,经过一天多的飞行,4月22日中午,天舟一号与天宫二号空间实验室进行自动交会对接,形成组合体,某商家根据市场预测,购进“天舟一号”(记作A)、“天宫二号”(记作B)两种航天模型,若购进A种模型10件,B种模型5件,需要1000元;若购进A种模型4件,B种模型3件,需要550元.
(1)求购进A,B两种模型每件需多少元?
(2)若该商店决定拿出1万元全部用来购进这两种模型,考虑到市场需求,要求购进A种模型的数量不超过B种模型数量的8倍,且B种模型最多购进33件,那么该商店共有几种进货方案?
(3)若销售每件A种模型可获利润20元,每件B种模型可获利润30元,在第(2)问的前提下,设销售总盈利为W元,购买B种模型m件,请求出W关于x的函数关系式,并求出当m为何值时,销售总盈利最大,并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列命题中为真命题的是( )
① ![]() 的算术平方根是4;
的算术平方根是4;
②若ma2>na2 , 则m>n;
③正八边形的一个内角的度数是135°;
④对角线互相垂直平分的四边形是菱形;
⑤平分弦的直径垂直于弦.
A.①③④
B.②③⑤
C.①④⑤
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角板ABC中,∠ACB=90°,∠B=30°,AC=2 ![]() ,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( )
,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( ) 
A.![]() π
π
B.![]() π
π
C.2π
D.3π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,D是△ABC的边BC上的一点,且CD=AB,∠BDA=∠BAD,AE是△ABD的中线.
⑴若∠B=60°,求∠C的值;
⑵求证:AD是∠EAC的平分线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了调查学生对雾霾天气的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了如图所示的不完整的三种统计图表.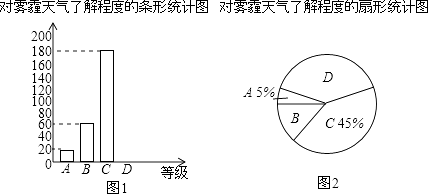
对雾霾的了解程度 | 百分比 |
A.非常了解 | 5% |
A.比较了解 | 15% |
C.基本了解 | 45% |
D.不了解 | n |
请结合统计图表,回答下列问题:
(1)本次参与调查的学生共有人,n=;扇形统计图中D部分扇形所对应的圆心角是度;
(2)请补全条形统计图;
(3)根据调查结果,学校准备开展关于雾霾的知识竞赛,某班要从“非常了解”程度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去,否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,FG∥EB,∠2=∠3,那么∠EDB+∠DBC等于多少度?为什么?

解:因为FG∥EB(已知),
所以![]() (__________).
(__________).
因为![]() (已知),
(已知),
所以![]() (___________).
(___________).
所以DE∥BC (__________).
所以![]() ______(__________).
______(__________).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com