

���� ��1���ɵȱ������ε����ʿ������B��C�����꣬�����ô���ϵ��������������ߵĽ���ʽ��
��2����t�ɷֱ��ʾ��BP��AP��AQ����Rt��APQ�У��ɵõ�AQ=2AP���ɵõ�����t�ķ��̣������t��ֵ��
��3����E�����AB�ĶԳƵ�E�䣬��֪E����OB�ϣ���F���ڶԳ���ĶԳƵ�F�䣬����E��F�䣬�ֱ�AB��G�����Գ�����H����E��F��=EG+GH+HF����ʱ�ı���EGHF���ܳ���С����E�䡢F��ֱ���x��Ĵ��ߣ��ɷֱ����E�䡢F������꣬�����E��F��ij���������ı���EGHF���ܳ�����Сֵ��
��� �⣺
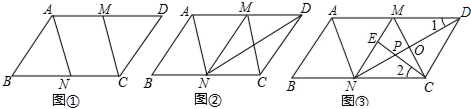
��1����ͼ1������OB���ֱ���BM��x�ᣬCN��x�ᣬ����ֱ�ΪM��N��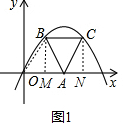
��BC��x�ᣬ��ABCΪ�ȱ������Σ�
���BAO=��ABC=60�㣬OA=AB=BC=6��
���OABΪ�ȱ������Σ�
��OM=$\frac{1}{2}$OA=3��BM=$\frac{\sqrt{3}}{2}$OB=3$\sqrt{3}$=CN����ON=OM+MN=OM+BC=9��
��B��3��3$\sqrt{3}$����C��9��3$\sqrt{3}$����
�������߹�ԭ��O��
����������߽���ʽΪy=ax2+bx��
��B��C�������ɵ�$\left\{\begin{array}{l}{9a+3b=3\sqrt{3}}\\{81a+9b=3\sqrt{3}}\end{array}\right.$����$\left\{\begin{array}{l}{a=-\frac{\sqrt{3}}{9}}\\{b=\frac{4\sqrt{3}}{3}}\end{array}\right.$��
�������߽���ʽΪy=-$\frac{\sqrt{3}}{9}$x2+$\frac{4\sqrt{3}}{3}$x��
��2����ͼ2������PQ��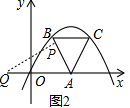
�������֪BP=2t��OQ=t����AP=6-2t��AQ=6+t��
��PQ��ABʱ���ڡ�APQ�У���PQA=30�㣬
��AQ=2AP��
��6+t=2��6-2t�������t=$\frac{6}{5}$��
�൱t��ֵΪ$\frac{6}{5}$ʱ��PQ��AB��
��3����ͼ3����E�����AB�ĶԳƵ�E�䣬��֪E����OB�ϣ���F���ڶԳ���ĶԳƵ�F�䣬����E��F�䣬�ֱ�AB��G�����Գ�����H��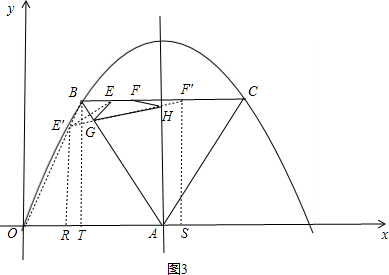
��EG=E��G��FH=F��H��
���߶���̿�֪��ʱEG+GH+FH=E��F�䣬
���ʱ��G��H��Ϊ���������ĵ㣬���ı���EGHF���ܳ���С��
�ֱ��E�䣬F�䣬B��x��Ĵ��ߣ�����ֱ�ΪR��S��T��
�ɣ�1����֪BT=F��S=3$\sqrt{3}$��
��BE=EF=1��
��BE��=1����OE��=OB-BE��=5��AS=1��
��OS=OA+1=7��
��F��������7��3$\sqrt{3}$����
�ڡ�ORE���У�OR=$\frac{1}{2}$OE��=$\frac{5}{2}$��RE��=$\frac{\sqrt{3}}{2}$OE��=$\frac{5\sqrt{3}}{2}$��
��E��������$\frac{5}{2}$��$\frac{5\sqrt{3}}{2}$����
��E��F��=$\sqrt{��7-\frac{5}{2}��^{2}+��3\sqrt{3}-\frac{5\sqrt{3}}{2}��^{2}}$=$\sqrt{21}$��
��EF=1��
���ı���EGHF���ܳ���Сֵ=EF+E��F��=1+$\sqrt{21}$��
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰֪ʶ���д���ϵ�������ȱ������ε����ʡ�ֱ�������ε����ʡ���ԳƵ����ʵȣ��ڣ�1�������B��C��������ǽ���Ĺؼ����ڣ�2���а������߶���t��ʾ��������Ϊ�����ڣ�3����ȷ����G��H��λ���ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Ժ�ǿ���ر��ǵڣ�3�����Ǹ��ѵ㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016-2017ѧ�꽭��ʡ���ھ��꼶��һ���¿���ѧ�Ծ��������棩 ���ͣ������
���� ��(2x��2y)��________��
��(2x��2y)��________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ��㶫ʡ���꼶��ѧ�ڵ�һ���¿���ѧ�Ծ��������棩 ���ͣ������
 ��_____��_____��ʽ����������_____����ߴ�����_____��
��_____��_____��ʽ����������_____����ߴ�����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 5 | C�� | 6 | D�� | 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
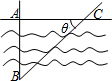 ��ͼ��Ϊ�˲���������A��B����ľ��룬����AB��ֱ�ķ����C�����AC=a����ACB=�ȣ���ôAB���ڣ�������
��ͼ��Ϊ�˲���������A��B����ľ��룬����AB��ֱ�ķ����C�����AC=a����ACB=�ȣ���ôAB���ڣ�������| A�� | a•sin�� | B�� | a•tan�� | C�� | a•cos�� | D�� | $\frac{a}{tan��}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com