
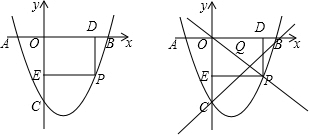
分析 (1)利用待定系数即可求解;
(2)根据P在抛物线上,则可用m表示出n,则四边形的周长即可求解;
(3)首先求得线段BC的解析式,即可得到△OBC是等腰直角三角形,然后分OC是底边,CQ是底边和OQ是底边三种情况进行讨论,即可求解.
解答 解:(1)根据题意得:$\left\{\begin{array}{l}{4a-2b-5=0}\\{25a+5b-5=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-\frac{3}{2}}\end{array}\right.$,
则抛物线的解析式是:y=$\frac{1}{2}$x2-$\frac{3}{2}$x-5;
(2)P(m,n)在抛物线上,则n=$\frac{1}{2}$m2-$\frac{3}{2}$m-5,
则l=2m-2($\frac{1}{2}$m2-$\frac{3}{2}$m-5),即l=-m2+5m+10=-(m-$\frac{5}{2}$)2+$\frac{65}{4}$.
l≤$\frac{65}{4}$,即l的最大值为$\frac{65}{4}$.
(3)在y=$\frac{1}{2}$x2-$\frac{3}{2}$x-5中,令x=0,解得y=-5,则C的坐标是(0,-5),则OC=OB=5.
设线段BC的解析式是y=kx+b,
则$\left\{\begin{array}{l}{5k+b=0}\\{b=-5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=-5}\end{array}\right.$,
则线段BC的解析式是y=x-5(0<x<5).
当OC时等腰三角形的底边时,即OQ=CQ时,则Q的坐标是-$\frac{5}{2}$,把y=-$\frac{5}{2}$代入y=x-5得:x=$\frac{5}{2}$,则Q的坐标是($\frac{5}{2}$,-$\frac{5}{2}$);
当CQ是等腰三角形的底边,即OC=OQ时,此时Q和B重合,不符合题意;
当OQ是等腰三角形的底边,即OC=CQ时,CQ=5,且∠OCQ=45°,作QF⊥y轴于点F.
则CF=QF=$\frac{5\sqrt{2}}{2}$,则OF=5-$\frac{5\sqrt{2}}{2}$=$\frac{10-5\sqrt{2}}{2}$,
则Q的坐标是($\frac{5\sqrt{2}}{2}$,$\frac{5\sqrt{2}-10}{2}$).
总之,Q的坐标是:($\frac{5}{2}$,-$\frac{5}{2}$)或($\frac{5\sqrt{2}}{2}$,$\frac{5\sqrt{2}-10}{2}$).
点评 本题考查了待定系数法求函数的解析式以及等腰三角形的讨论,正确进行讨论是本题的关键.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 在一个标准大气压下,加热到100℃,水沸腾 | |
| B. | 购买一张福利彩票,中奖 | |
| C. | -2的绝对值小于0 | |
| D. | 在一个仅装着白球和黑球的袋中摸球,摸出红球 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
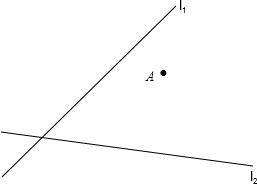 如图,点A表示城镇,直线l1,l2表示两条相交的公路,电信部门要修建一座信号发射塔P,按照设计要求,发射塔到两条公路l1,l2的距离必须相等,且使发射塔P到A的距离最短,请用尺规作图确定发射塔P的位置(保留作图痕迹,不要求写出画法)
如图,点A表示城镇,直线l1,l2表示两条相交的公路,电信部门要修建一座信号发射塔P,按照设计要求,发射塔到两条公路l1,l2的距离必须相等,且使发射塔P到A的距离最短,请用尺规作图确定发射塔P的位置(保留作图痕迹,不要求写出画法)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
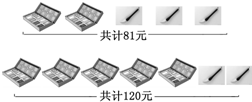 某校为表彰在美术展览活动中获奖的同学,老师决定购买一些水笔和颜料盒作为奖品,请你根据图中所给的信息,解答下列问题;
某校为表彰在美术展览活动中获奖的同学,老师决定购买一些水笔和颜料盒作为奖品,请你根据图中所给的信息,解答下列问题;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com