
| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 价格y1(元/件) | 560 | 580[ | 600 | 620 | 640 | 660 | 680 | 700 | 720 |

 ,解得
,解得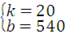 ,
,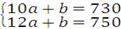 ,解得
,解得 ,
,

科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 倍,正好按期完工。若用横轴表示工期,纵轴表示未完成的工程量,下面能反映这段工程的图像是( ).
倍,正好按期完工。若用横轴表示工期,纵轴表示未完成的工程量,下面能反映这段工程的图像是( ).
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题


查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题


查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 月销量x(件) | 1500 | 2000 |
| 销售价格y(元/件) | 185 | 180 |
 (元)
(元) x2元的附加费,设月利
x2元的附加费,设月利 (元)(利润=销售额-成本-附加费).
(元)(利润=销售额-成本-附加费). ,
, 与x间的函数关系式(不必写x的取值范围);
与x间的函数关系式(不必写x的取值范围);查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 =
= 代入,这个函数将失去意义,我们把这样的数值
代入,这个函数将失去意义,我们把这样的数值 叫做自变量x的奇异值,请写出一个函数,使2和-2都是这个函数的奇异值,你写出的函数为 ▲ .
叫做自变量x的奇异值,请写出一个函数,使2和-2都是这个函数的奇异值,你写出的函数为 ▲ .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com