
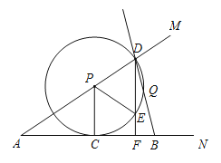
【题目】已知点P为∠MAN边AM上一动点,⊙P切AN于点C,与AM交于点D(点D在点P的右侧),作DF⊥AN于F,交⊙O于点E.
(1)连接PE,求证:PC平分∠APE;
(2)若DE=2EF,求∠A的度数;
(3)点B为射线AN上一点,且AB=8,射线BD交⊙P于点Q,sin∠A=![]() .在P点运动过程中,是否存在某个位置,使得△DQE为等腰三角形?若存在,求出此时AP的长;若不存在,请说明理由.
.在P点运动过程中,是否存在某个位置,使得△DQE为等腰三角形?若存在,求出此时AP的长;若不存在,请说明理由.
【答案】(1)证明见解析;(2)∠PAC=30°;(3)存在,AP的长为6或![]() 或
或![]() .
.
【解析】
(1)根据已知条件以及切线的性质可得PC//DF,再利用平行线的性质和等腰三角形的性质可以证得∠APC=∠EPC,即可得证结论;
(2)添加辅助线PH⊥DE于H,根据已知条件可得DH=HE=EF=![]() HF=
HF=![]() PC=
PC=![]() PD,进一步可判定∠DPH=30°,最后利用平行线的性质即可推导出∠A的度数;
PD,进一步可判定∠DPH=30°,最后利用平行线的性质即可推导出∠A的度数;
(3)分①DQ=QE②DE=QE③DQ=DE三种情况进行讨论即可.
解:(1)证明:∵AN切⊙O于点C
∴PC⊥AN
∵DF⊥AN
∴PC//DF
∴∠APC=∠PDE, ∠EPC=∠PED
∵PD=PE
∴∠PED=∠PDE
∴∠APC=∠EPC,即PC平分∠APE
(2)作PH⊥DE于H,如图:
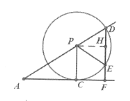
∵PD=PE,DE=2EF
∴DH=HE=EF=![]() HF=
HF=![]() PC=
PC=![]() PD
PD
∴∠DPH=30°
∵PH//AF
∴∠PAC=∠DPH=30°
(3)①当DQ=QE时,如图1

连接PQ,可证得PQ//AB
∴∠PDQ=∠DQP=∠DBA
∴AD=AB=8
∵设PC=r,AP=3r
∴AD=4r
∴4r=8
∴r=2
∴AP=3r=6
②当DE=QE时, 记⊙P与AD的另一交点为K,连接KE,如图:

则∠QDE=∠EQD=∠DKE=∠DAF
在Rt△ADF中,DF=![]() AD=
AD=![]() r
r
AF=![]() DF=
DF=![]() r
r
在Rt△DBF中,BF=![]() DF=
DF=![]() r
r
AB=AF-BF=![]() r=8
r=8
r=![]() ,AP=3r=
,AP=3r=![]()
③当DQ=DE时,连接QK连接QE交AD于I,作QG⊥KE于点G,如图:

则∠GQE=∠IKE=∠A
在Rt△QGE中,设GE=2x,则QE=3GE=6x,IE=3x
QG=![]() GE=
GE=![]() x
x
则KG=KE-EG=7x
tan∠QKG=![]() =
=![]() ,
,
∵∠BDF=∠QKE
∴ tan∠BDF= tan∠QKE,BF=![]() DF=
DF=![]()
AB=AF+BF=![]() =8,
=8,
r=![]() ,AP=3r=
,AP=3r=![]()
故答案是:(1)证明见解析;(2)∠PAC=30°;(3)存在,AP的长为6或![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,A,B两个顶点在x轴上方,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,得到△A'B'C',设点B的对应点B'的横坐标为2,则点B的横坐标为( )
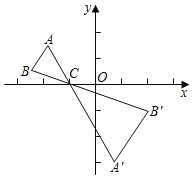
A.﹣1B.![]() C.﹣2D.
C.﹣2D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着经济的快速发展,环境问题越来越受到人们的关注.某校学生会为了了解垃圾分类知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,并将调查结果绘制成下面两幅统计图.
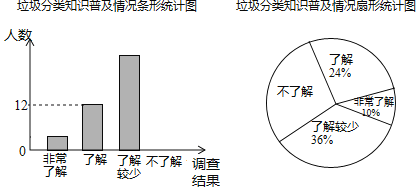
(1)求:本次被调查的学生有多少名?补全条形统计图.
(2)估计该校1200名学生中“非常了解”与“了解”的人数和是多少.
(3)被调查的“非常了解”的学生中有2名男生,其余为女生,从中随机抽取2人在全校做垃圾分类知识交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系 XOY中,对于任意两点 ![]() (
(![]() ,
,![]() )与
)与 ![]() (
(![]() ,
,![]() )的“非常距离”,给出如下定义: 若
)的“非常距离”,给出如下定义: 若 ![]() ,则点
,则点 ![]() 与点
与点 ![]() 的“非常距离”为
的“非常距离”为 ![]() ;若
;若 ![]() ,则点
,则点 ![]() 与点
与点![]() 的“非常距离”为
的“非常距离”为 ![]() .
.
例如:点 ![]() (1,2),点
(1,2),点 ![]() (3,5),因为
(3,5),因为 ![]() ,所以点
,所以点 ![]() 与点
与点 ![]() 的“非常距离”为
的“非常距离”为 ![]() ,也就是图1中线段
,也就是图1中线段 ![]() Q与线段
Q与线段 ![]() Q长度的较大值(点 Q为垂直于 y轴的直线
Q长度的较大值(点 Q为垂直于 y轴的直线 ![]() Q与垂直于 x轴的直线
Q与垂直于 x轴的直线 ![]() Q的交点)。
Q的交点)。
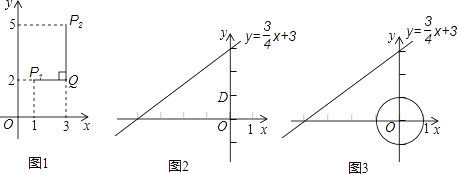
(1)已知点 A(-![]() ,0), B为 y轴上的一个动点,①若点 A与点 B的“非常距离”为2,写出一个满足条件的点 B的坐标;②直接写出点 A与点 B的“非常距离”的最小值;
,0), B为 y轴上的一个动点,①若点 A与点 B的“非常距离”为2,写出一个满足条件的点 B的坐标;②直接写出点 A与点 B的“非常距离”的最小值;
(2)已知 C是直线 ![]() 上的一个动点,①如图2,点 D的坐标是(0,1),求点 C与点 D的“非常距离”的最小值及相应的点 C的坐标; ②如图3, E是以原点 O为圆心,1为半径的圆上的一个动点,求点 C与点 E的“非常距离”的最小值及相应的点 E和点 C的坐标。
上的一个动点,①如图2,点 D的坐标是(0,1),求点 C与点 D的“非常距离”的最小值及相应的点 C的坐标; ②如图3, E是以原点 O为圆心,1为半径的圆上的一个动点,求点 C与点 E的“非常距离”的最小值及相应的点 E和点 C的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
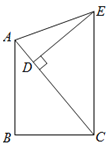
【题目】如图,△ABC为直角三角形,∠B=90°,AC边上取一点D,使CD=AB.分别过点C作CE⊥BC,过点D作DE⊥AC,CE,DE相交于E,连结AE.
(1)求证:△ABC≌△CDE;
(2)若∠AED=20°,求∠ACE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂用![]() 天时间生产一款新型节能产品,每天生产的该产品被某网店以每件
天时间生产一款新型节能产品,每天生产的该产品被某网店以每件![]() 元的价格全部订购,在生产过程中,由于技术的不断更新,该产品第
元的价格全部订购,在生产过程中,由于技术的不断更新,该产品第![]() 天的生产成本
天的生产成本![]() (元/件)与
(元/件)与![]() (天)之间的关系如图所示,第
(天)之间的关系如图所示,第![]() 天该产品的生产量
天该产品的生产量![]() (件)与
(件)与![]() (天)满足关系式
(天)满足关系式![]()
![]() 第
第![]() 天,该厂生产该产品的利润是 元;
天,该厂生产该产品的利润是 元;
![]() 设第
设第![]() 天该厂生产该产品的利润为
天该厂生产该产品的利润为![]() 元.
元.
①求![]() 与
与![]() 之间的函数关系式,并指出第几天的利润最大,最大利润是多少?
之间的函数关系式,并指出第几天的利润最大,最大利润是多少?
②在生产该产品的过程中,当天利润不低于![]() 元的共有多少天?
元的共有多少天?

查看答案和解析>>
科目:初中数学 来源: 题型:
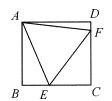
【题目】如图,在矩形 ABCD 中,点 E,F 分别在 BC,CD 边上,且 CE=3,CF=4.若△AEF 是等边三角形,则 AB 的长为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点E,F,G分别是等边三角形ABC三边AB,BC,CA上的动点,且始终保持AE=BF=CG,设△EFG的面积为y,AE的长为x,y关于x的函数图象大致为图2所示,则等边三角形ABC的边长为___.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com