
 然不一定,错误.
然不一定,错误.

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
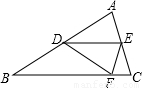
 24、(1)如图,△ABC纸片中,∠A=36°,AB=AC,请你剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形.请画出示意图,并标明必要的角度;
24、(1)如图,△ABC纸片中,∠A=36°,AB=AC,请你剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形.请画出示意图,并标明必要的角度;查看答案和解析>>
科目:初中数学 来源: 题型:
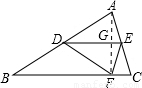
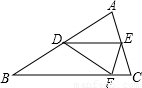
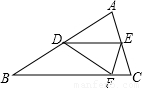
 27、如图,△ABC纸片中,AB=BC>AC,点D是AB边的中点,点E在边AC上,将纸片沿DE折叠,使点A落在BC边上的点F处.则下列结论成立的个数有( )
27、如图,△ABC纸片中,AB=BC>AC,点D是AB边的中点,点E在边AC上,将纸片沿DE折叠,使点A落在BC边上的点F处.则下列结论成立的个数有( )查看答案和解析>>
科目:初中数学 来源:第4章《视图与投影》易错题集(40):4.1 视图(解析版) 题型:选择题
查看答案和解析>>
科目:初中数学 来源:2009年浙江省宁波市江东区初中毕业生学业质量抽测数学试卷(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com