
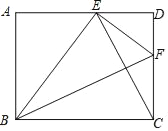
【题目】如图,在矩形ABCD中,点E是边AD上的点,EF⊥BE,交边CD于点F,联结CE、BF,如果tan∠ABE=![]() ,那么CE:BF=_____.
,那么CE:BF=_____.
【答案】4:5
【解析】
首先证明B,C,F,E四点共圆,推出∠EBF=∠ECF,推出△BEF∽△CDE,可得![]() =
=![]() ,再证明∠DEF=∠ABE,推出tan∠ABE=tan∠DEF=
,再证明∠DEF=∠ABE,推出tan∠ABE=tan∠DEF=![]() =
=![]() ,设DF=3k,DE=4k,可得EF=5k,由此即可解决问题.
,设DF=3k,DE=4k,可得EF=5k,由此即可解决问题.
解:∵四边形ABCD是矩形,
∴∠A=∠D=∠BCD=90°,
∵EF⊥BE,
∴∠BEF=90°,
∴∠BEF+∠BCF=180°,
∴B,C,F,E四点共圆,
∴∠EBF=∠ECF,∵∠BEF=∠D=90°,
∴△BEF∽△CDE,
∴![]() =
=![]() ,
,
∵∠ABE+∠AEB=90°,∠AEB+∠DEF=90°,
∴∠DEF=∠ABE,
∴tan∠ABE=tan∠DEF=![]() =
=![]() ,
,
设DF=3k,DE=4k,
∴EF=5k,
∴![]() =
=![]() =
=![]() ,
,
故答案为:4:5.


科目:初中数学 来源: 题型:
【题目】某商店销售一种成本为20元的商品,经调研,当该商品每件售价为30元时,每天可销售200件:当每件的售价每增加1元,每天的销量将减少5件.
![]() 求销量
求销量![]() 件
件![]() 与售价
与售价![]() 元
元![]() 之间的函数表达式;
之间的函数表达式;
![]() 如果每天的销量不低于150件,那么,当售价为多少元时,每天获取的利润最大,最大利润是多少?
如果每天的销量不低于150件,那么,当售价为多少元时,每天获取的利润最大,最大利润是多少?
![]() 该商店老板热心公益事业,决定从每天的销售利润中捐出100元给希望工程,为保证捐款后每天剩余利润不低于2900元,请直接写出该商品售价的范围.
该商店老板热心公益事业,决定从每天的销售利润中捐出100元给希望工程,为保证捐款后每天剩余利润不低于2900元,请直接写出该商品售价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△A1B1C1是位似图形.
(1)在网格上建立平面直角坐标系,使得点A的坐标为(﹣6,﹣1),点C1的坐标为(﹣3,2),则点B的坐标为 ;
(2)以点A为位似中心,在网格图中作△AB2C2,使△AB2C2和△ABC位似,且位似比为1:2;
(3)在图上标出△ABC与△A1B1C1的位似中心P,并写出点P的坐标为 ,计算四边形ABCP的周长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,点D在边AC上,BD的垂直平分线交CA的延长线于点E,交BD于点F,联结BE,ED2=EAEC.
(1)求证:∠EBA=∠C;
(2)如果BD=CD,求证:AB2=ADAC.

查看答案和解析>>
科目:初中数学 来源: 题型:
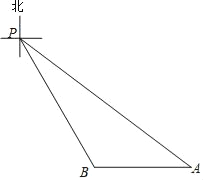
【题目】如图,P点是某海域内的一座灯塔的位置,船A停泊在灯塔P的南偏东53°方向的50海里处,船B位于船A的正西方向且与灯塔P相距20![]() 海里.(本题参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)
海里.(本题参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)
(1)试问船B在灯塔P的什么方向?
(2)求两船相距多少海里?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
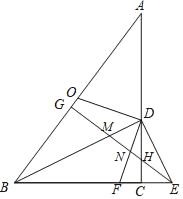
【题目】在△ABC中,∠ACB=90°,BC=3,AC=4,点O是AB的中点,点D是边AC上一点,DE⊥BD,交BC的延长线于点E,OD⊥DF,交BC边于点F,过点E作EG⊥AB,垂足为点G,EG分别交BD、DF、DC于点M、N、H.
(1)求证:![]() ;
;
(2)设CD=x,NE=y,求y关于x的函数关系式及其定义域;
(3)当△DEF是以DE为腰的等腰三角形时,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,BC=8.动点P从点A出发沿AC向终点C运动,同时动点Q从点B出发沿BA向点A运动,到达A点时停止运动.点P也同时停止.点P,Q运动速度均为每秒1个单位长度,连接PQ,设运动时间为t(t>0)秒.
(1)当点Q从B点向A点运动时(未到达A点),
①当t=_____时PQ∥BC
②求△APQ的面积S关于t的函数关系式,并写出t的取值范围;
(2)伴随着P,Q两点的运动,线段PQ的垂直平分线为l:
①当l经过点A时,射线QP交AD于点E,求此时的t的值和AE的长;
②当l经过点B时,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
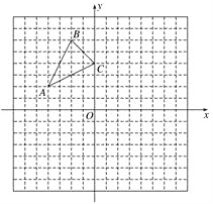
【题目】如图,已知A(-4,2),B(-2,6),C(0,4)是直角坐标系平面上三点.
(1)把△ABC向右平移4个单位再向下平移1个单位,得到△A1B1C1,画出平移后的图形;
(2)若△ABC内部有一点P(a,b),则平移后它的对应点P1的坐标为__________;
(3)以原点O为位似中心,将△ABC缩小为原来的一半,得到△A2B2C2,请在所给的坐标系中作出所有满足条件的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
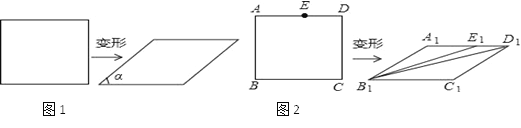
我们知道,四边形具有不稳定性,容易变形,如图1,一个矩形发生变形后成为一个平行四边形,设这个平行四边形相邻两个内角中较小的一个内角为α,我们把![]() 的值叫做这个平行四边形的变形度.
的值叫做这个平行四边形的变形度.
(1)若矩形发生变形后的平行四边形有一个内角是120度,则这个平行四边形的变形是 .
猜想证明:
(2)设矩形的面积为S1,其变形后的平行四边形面积为S2,试猜想S1,S2, ![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
拓展探究:
(3)如图2,在矩形ABCD中,E是AD边上的一点,且AB2=AEAD,这个矩形发生变形后为平行四边形A1B1C1D1,E1为E的对应点,连接B1E1,B1D1,若矩形ABCD的面积为4![]() (m>0),平行四边形A1B1C1D1的面积为2
(m>0),平行四边形A1B1C1D1的面积为2![]() (m>0),试求∠A1E1B1+∠A1D1B1的度数.
(m>0),试求∠A1E1B1+∠A1D1B1的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com