
【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m) 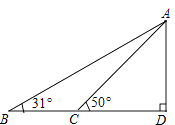
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.
【答案】
(1)解:在Rt△ABD中,AD=24m,∠B=31°,
∴tan31°= ![]() ,即BD=
,即BD= ![]() =40m,
=40m,
在Rt△ACD中,AD=24m,∠ACD=50°,
∴tan50°= ![]() ,即CD=
,即CD= ![]() =20m,
=20m,
∴BC=BD﹣CD=40﹣20=20m,
则B,C的距离为20m;
(2)解:根据题意得:20÷2=10m/s<15m/s,
则此轿车没有超速
【解析】(1)在直角三角形ABD与直角三角形ACD中,利用锐角三角函数定义求出BD与CD的长,由BD﹣CD求出BC的长即可;(2)根据路程除以时间求出该轿车的速度,即可作出判断.此题考查了解直角三角形的应用,熟练掌握锐角三角函数定义是解本题的关键.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2![]() =(1+
=(1+![]() )2,善于思考的小明进行了以下探索:
)2,善于思考的小明进行了以下探索:
设a+b![]() =(m+n
=(m+n![]() )2(其中a、b、m、n均为整数),则有a+b
)2(其中a、b、m、n均为整数),则有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() ,∴a=m2+2n2,b=2mn,这样小明就找到了一种把部分a+b
,∴a=m2+2n2,b=2mn,这样小明就找到了一种把部分a+b![]() 的式子化为平方式的方法。
的式子化为平方式的方法。
请我仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b![]() =(m+n
=(m+n![]() )2,用含m、n的式子分别表示a、b,得a=________, b=___________.
)2,用含m、n的式子分别表示a、b,得a=________, b=___________.
(2)若a+4![]() =(m+n
=(m+n![]() )2,且a、m、n均为正整数,求a的值。
)2,且a、m、n均为正整数,求a的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某镇水库的可用水量为12000万m3,假设年降水量不变,能维持该镇16万人20年的用水量.为实施城镇化建设,新迁入了4万人后,水库只能够维持居民15年的用水量.
(1)问:年降水量为多少万m3?每人年平均用水量多少m3?
(2)政府号召节约用水,希望将水库的使用年限提高到25年.则该镇居民人均每年需节约多少m3水才能实现目标?
(3)某企业投入1000万元设备,每天能淡化5000m3海水,淡化率为70%.每淡化1m3海水所需的费用为1.5元,政府补贴0.3元.企业将淡化水以3.2元/m3的价格出售,每年还需各项支出40万元.按每年实际生产300天计算,该企业至少几年后能收回成本(结果精确到个位)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋中装有一红一白2个球,这些球除颜色外都相同,小刚从袋中随机摸出一个球,记下颜色后放回袋中,再从袋中随机摸出一个球,两次都摸到红球的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆市2017年女子迷你马拉松比赛在南滨路举行,王老师和刘老师参加了比赛,图中AB、OC分别表示王老师和刘老师前往终点所跑的路程S(km)随时间t(min)变化的函数图象,以下说法:①这是全长为5km的比赛;②王老师比刘老师早15分钟到达终点;③王老师出发15分钟时遇到刘老师;④王老师的平均速度为500米/分钟.其中正确的有( )

A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
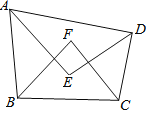
【题目】如图,四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E,∠ABC、∠BCD的角平分线交于点F.
(1)若∠F=70°,则∠ABC+∠BCD= ______ °;∠E= ______ °;
(2)探索∠E与∠F有怎样的数量关系,并说明理由;
(3)给四边形ABCD添加一个条件,使得∠E=∠F,所添加的条件为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC 中,AB=AC=6cm,∠B=∠C,BC=4cm,点 D 为 AB的中点.
(1)如果点 P 在线段 BC 上以 1cm/s 的速度由点 B 向点 C 运动,同时,点 Q 在线段 CA 上由点 C 向点 A 运动.
①若点 Q 的运动速度与点 P 的运动速度相等,经过 1 秒后,△BPD 与△CQP 是否全等,请说明理由;
②若点 Q 的运动速度与点 P 的运动速度不相等,当点 Q 的运动速度为多少时,能够使△BPD 与△CQP 全等?
(2)若点 Q 以②中的运动速度从点 C 出发,点 P 以原来的运动速度从点 B 同时出发,都逆时针沿△ABC 三边运动,则经过 后,点 P 与点 Q 第一次在△ABC 的 边上相遇?(在横线上直接写出答案,不必书写解题过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是一片水田,某村民小组需计算其面积,测得如下数据:
∠A=90°,∠ABD=60°,∠CBD=54°,AB=200m,BC=300m.
请你计算出这片水田的面积.
(参考数据:sin54°≈0.809,cos54°≈0.588,tan54°≈1.376, ![]() ≈1.732)
≈1.732)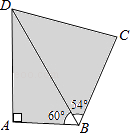
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com