
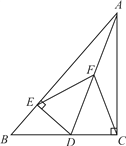
【题目】如图,在Rt△ABC中,∠ACB=90°,D是边BC上一点,DE⊥AB于点E,点F是线段AD上一点,连结EF、CF.
(1)若AD平分∠BAC,求证:EF=CF.
(2)若点F是线段AD的中点,试猜想线段EF与CF的大小关系,并加以证明.
(3)在(2)的条件下,若∠BAC=45°,AD=6,直接写出C、E两点间的距离.
【答案】(1)证明见解析;(2)EF=CF.理由见解析;(3)![]() .
.
【解析】试题分析:(1)由AD平分∠BAC,DE⊥AB,∠ACB=90°可得:∠1 =∠2,∠1+∠3=90°,∠2+∠4=90°,DE= DC,则∠3=∠4,则在△DEF≌△DCF,再根据全等三角形的性质可得出EF=CF;(2)在Rt△AED和Rt△ACD中,由点F是线段AD的中点可得: ![]() ,
, ![]() ,所以EF=CF;(3)由AD=6,EF=CF=
,所以EF=CF;(3)由AD=6,EF=CF=![]() AD=AF=DF=3可得:∠DFE=2∠FAE,∠CFD=2∠CAF,所以∠EFC=2∠CAE=90°,即△CEF是直角三角形,所以CE=
AD=AF=DF=3可得:∠DFE=2∠FAE,∠CFD=2∠CAF,所以∠EFC=2∠CAE=90°,即△CEF是直角三角形,所以CE=![]() ;
;
试题解析:
(1)如图所示:

∵AD平分∠BAC,DE⊥AB,∠ACB=90°,
∴∠1 =∠2,∠1+∠3=90°,∠2+∠4=90°,DE= DC.
∴∠3=∠4.
∵DF = DF,
∴△DEF≌△DCF.
∴EF=CF.
(2)EF=CF. (只写结论给1分)
在Rt△AED和Rt△ACD中,
∵点F是线段AD的中点,
∴![]() ,
, ![]() ,
,
∴EF=CF. \
(3)![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图:AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:①∠BOE=70°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论有( ) 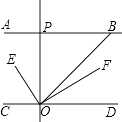
A.①②③④
B.①②③
C.①③④
D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直接写出结果
(1)﹣8﹣2=
(2)2.5﹣(﹣7.5)=
(3)![]() ﹣1=
﹣1=
(4)12÷(- ![]() )=
)=
(5)(﹣0.8)×(﹣2)=
(6)(﹣2)3=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪计划中考后参加“我的中国梦”夏令营活动,需要一名家长陪同,爸爸、妈妈用猜拳的方式确定由谁陪同,即爸爸、妈妈随机做出“石头”、 “剪刀”“布” 三种手势中的一种,规定:“石头”胜“剪刀”,“剪刀” 胜“布”,“布” 胜“石头”,手势相同,不分胜负.
(1)爸爸一次出“石头”的概率是多少?
(2)妈妈一次获胜的概率是多少?请用列表或画树状图的方法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD的外侧,以四边形的边为边分别作四个小正方形,连接相邻的两个顶点,得到四个阴影三角形,则这四个阴影三角形的面积a、b、c、d满足( ) 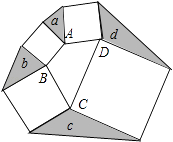
A.a+b=c+d
B.a2+b2=c2+d2
C.a+c=b+d
D.a2+c2=b2+d2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各为多少元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元.则有哪几种购车方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com