
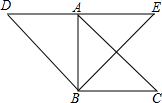
 如图,△ABC和△DBE为等腰直角三角形,且AD=2,AE=2$\sqrt{3}$,求AC的长.
如图,△ABC和△DBE为等腰直角三角形,且AD=2,AE=2$\sqrt{3}$,求AC的长. 分析 首先根据AD=2,AE=2$\sqrt{3}$,求出DE的长是多少;再根据△DBE为等腰直角三角形,求出BD的长是多少;然后在△ABD中,根据余弦定理,求出AB的长是多少;最后根据△ABC为等腰直角三角形,求出AC的长是多少即可.
解答 解:∵AD=2,AE=2$\sqrt{3}$,
∴DE=2+2$\sqrt{3}$,
∵△DBE为等腰直角三角形,
∴BD=(2+2$\sqrt{3}$)÷$\sqrt{2}$=$\sqrt{2}+\sqrt{6}$,∠ADB=45°,
在△ABD中,根据余弦定理,可得
AB2=AD2+BD2-2AD•BD•cos45°
=22${+(\sqrt{2}+\sqrt{6})}^{2}$$-2×2×(\sqrt{2}+\sqrt{6})$×$\frac{\sqrt{2}}{2}$
=4+8+$4\sqrt{3}$-4-4$\sqrt{3}$
=8
∴AB=2$\sqrt{2}$,
∵△ABC为等腰直角三角形,
∴AC=2$\sqrt{2}×\sqrt{2}$=4,
即AC的长是4.
点评 此题主要考查了等腰直角三角形的性质和应用,要熟练掌握,解答此题的关键是要明确:等腰直角三角形是一种特殊的三角形,具有所有三角形的性质,还具备等腰三角形和直角三角形的所有性质.即:两个锐角都是45°,斜边上中线、角平分线、斜边上的高,三线合一,等腰直角三角形斜边上的高为外接圆的半径R,而高又为内切圆的直径.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 筐 数 | 2 | 5 | 3 | 4 | 2 | 4 |
| 与标准重量比较(千克) | -0.8 | +0.6 | -0.5 | -0.4 | +0.5 | -0.3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
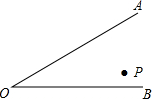 如图,已知P为∠AOB内任意一点,且∠AOB=30°,点P1、P2分别在OA、OB上,求作点P1、P2,使△PP1P2的周长最小,连接OP,若OP=10cm,求△PP1P2的周长.
如图,已知P为∠AOB内任意一点,且∠AOB=30°,点P1、P2分别在OA、OB上,求作点P1、P2,使△PP1P2的周长最小,连接OP,若OP=10cm,求△PP1P2的周长.查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次课堂调研数学试卷(解析版) 题型:填空题
如图,给出了过直线外一点作已知直线的平行线的方法,其依据是____________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com