

分析 (1)如图1,连接对角线OA、OB,证明△AOM≌△BON(ASA),则S△AOM=S△BON,所以S=S△ABO=$\frac{1}{4}$S正方形ABCD=$\frac{1}{4}$×4=1;
(2)如图2,在旋转过程中,∠α与正n边形重叠部分的面积S不变,连接OA、OB,同理证明△OAM≌△OBN,则S=S△OBN+S△OBM=S△OAM+S△OBM=S△OAB,故S的大小不变;
(3)如图3,120°相当于两个中心角,可以理解为一个中心角连续旋转两次,由前两问的推理得,旋转一个中心角时重叠部分的面积是原来正n边形面积的$\frac{1}{n}$,则S是原正六边形面积的$\frac{1}{3}$;也可以类比(1)(2)证明△OAM≌△OBN,利用割补法求出结论;
四边形OMPN是菱形,
理由如下:如图4,作∠α的平分线与BC边交于点P,作辅助线构建全等三角形,同理证明△OAM≌△OBP≌△OCN,得△OMP和△OPN都是等边三角形,则OM=PM=OP=ON=PN,根据四边相等的四边是菱形可得:四边形OMPN是菱形.
解答 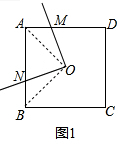 解:(1)如图1,连接OA、OB,
解:(1)如图1,连接OA、OB,
当n=4时,四边形ABCD是正方形,
∴OA=OB,AO⊥BO,
∴∠AOB=90°,
∴∠AON+∠BON=90°,
∵∠MON=∠α=90°,
∴∠AON+∠AOM=90°,
∴∠BON=∠AOM,
∵O是正方形ABCD的中心,
∴∠OAM=∠ABO=45°,
在△AOM和△BON中,
∵$\left\{\begin{array}{l}{∠OAM=∠ABO}\\{OA=OB}\\{∠AOM=∠BON}\end{array}\right.$,
∴△AOM≌△BON(ASA),
∴S△AOM=S△BON,
∴S△AOM+S△AON=S△BON+S△AON,
即S四边形ANDM=S△ABO=S,
∵正方形ABCD的边长为2,
∴S正方形ABCD=2×2=4,
∴S=S△ABO=$\frac{1}{4}$S正方形ABCD=$\frac{1}{4}$×4=1;
(2)如图2,在旋转过程中,∠α与正n边形重叠部分的面积S不变,
理由如下:连接OA、OB,
则OA=OB=OC,∠AOB=∠MON=72°,
∴∠AOM=∠BON,且∠OAB=∠OBC=54°,
∴△OAM≌△OBN,
∴四边形OMBN的面积:S=S△OBN+S△OBM=S△OAM+S△OBM=S△OAB,
故S的大小不变;
(3)猜想:S是原正六边形面积的$\frac{1}{3}$,理由是: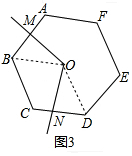
如图3,连接OB、OD,
同理得△BOM≌△DON,
∴S=S△BOM+S四边形OBCN=S△DON+S四边形OBCN=S四边形OBCD=$\frac{1}{3}$S六边形ABCDEF;
四边形OMPN是菱形,
理由如下:
如图4,作∠α的平分线与BC边交于点P,
连接OA、OB、OC、OD、PM、PN,
∵OA=OB=OC=OD,∠AOB=∠BOC=∠COD=∠MOP=∠PON=60°,
∴∠OAM=∠OBP=∠OCN=60°,∠AOM=∠BOP=∠CON,
∴△OAM≌△OBP≌△OCN,
∴OM=OP=ON,
∴△OMP和△OPN都是等边三角形,
∴OM=PM=OP=ON=PN,
∴四边形OMPN是菱形.
点评 本题考查了正n边形的性质、全等三角形的性质和判定、正n边形的中心角、中心等定义以及旋转等知识,明确正n边形的中心角=$\frac{360°}{n}$,熟练掌握全等三角形的性质和判定,难度适中,本题还运用了类比的思想解决数学问题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
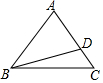 如图,△ABC中,AB=AC,点D在AC边上(不包括点A和点C),BD=BA,设∠A=x度,则x的取值范围是( )
如图,△ABC中,AB=AC,点D在AC边上(不包括点A和点C),BD=BA,设∠A=x度,则x的取值范围是( )| A. | 30<x<45 | B. | 45<x<60 | C. | 60<x<90 | D. | 90<x<120 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
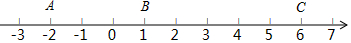
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,一半径为2的圆的圆心的初始位置在(0,2),此时圆上一点P的位置在(0,0),圆在x轴上以每秒$\frac{π}{3}$的速度沿x轴正方向滚动,8秒时P点到x轴的距离为3.
如图,在平面直角坐标系中,一半径为2的圆的圆心的初始位置在(0,2),此时圆上一点P的位置在(0,0),圆在x轴上以每秒$\frac{π}{3}$的速度沿x轴正方向滚动,8秒时P点到x轴的距离为3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,⊙O的半径为r.A,B为⊙O上的两个不同点;以B为圆心.BA为半径的圆交⊙O于另一点C.P为⊙O内一点,使得△PAB为正三角形,CP交⊙O于另一点Q.
如图,⊙O的半径为r.A,B为⊙O上的两个不同点;以B为圆心.BA为半径的圆交⊙O于另一点C.P为⊙O内一点,使得△PAB为正三角形,CP交⊙O于另一点Q.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com