
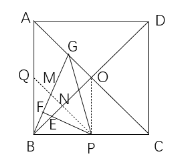
【题目】如图所示,已知正方形ABCD,对角线AC、BD交于点O,点P是边BC上一动点(不与点B、C重合),过点P作∠BPF,使得∠BPF=![]() ∠ACB,BG⊥PF于点F,交AC于点G,PF交BD于点E,给出下列结论,其中正确的是( )
∠ACB,BG⊥PF于点F,交AC于点G,PF交BD于点E,给出下列结论,其中正确的是( )
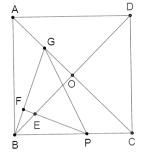
①![]() ;②PE=2BF;③在点P运动的过程中,当GB=GP时,
;②PE=2BF;③在点P运动的过程中,当GB=GP时,![]() ;④当P为BC的中点时,
;④当P为BC的中点时,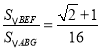 .
.
A.①②③B..①②④C.②③④D..①②③④
【答案】A
【解析】
①过G作GH⊥AB交于H点,得△BHG≌△BOG,HG=OG,解等腰直角三角形得![]() ;
;
②首先过P作PM∥AC交BG于M,交BO于N,易证得△BMN≌△PEN(ASA),△BPF≌△MPF(ASA),即可得BM=PE,BF=![]() BM,则可求得PE=2BF;
BM,则可求得PE=2BF;
③过P作PQ∥AC交BG于M,交BO于N,根据等腰直角三角形ABO的性质,可得![]() ,根据条件证得△PFG为等腰直角三角形,同理可证得
,根据条件证得△PFG为等腰直角三角形,同理可证得![]() ,由
,由![]() 即可证明;
即可证明;
④连接OP,则OP⊥BC,易知![]() ,根据①得
,根据①得![]() ,由△BEF∽△BGO,得
,由△BEF∽△BGO,得![]() ,进而得
,进而得![]() ,进而
,进而![]() ,整理即可求出结果.
,整理即可求出结果.
①过G作GH⊥AB交于H点,
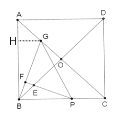
∵正方形ABCD,AC为对角线,
∴AG=![]() GH,
GH,
∵![]() ,
,![]() ,
,
∴△BHG≌△BOG,
∴HG=OG,
∴![]() ;
;
故①正确;
②如图2,过P作PM∥AC交BG于M,交BO于N,
∴∠PNE=∠BOC=90°,∠BPN=∠OCB.
∵∠OBC=∠OCB=45°,
∴∠NBP=∠NPB.
∴NB=NP.
∵∠MBN=90°∠BMN,∠NPE=90°∠BMN,
∴∠MBN=∠NPE,
在△BMN和△PEN中,
∠MBN=∠NPE,NB=NP,∠MNB=∠PNE=90°,
∴△BMN≌△PEN(ASA),
∴BM=PE,
∵∠BPE=
∴∠BPF=∠MPF.
∵PF⊥BM,
∴∠BFP=∠MFP=90°.
在△BPF和△MPF中,∠BPF=∠MPF,PF=PF,∠PFB=∠PFM,
∴△BPF≌△MPF(ASA).
∴BF=MF,
即BF=![]() BM
BM
∴BF=![]() PE,即PE=2BE;
PE,即PE=2BE;
故②正确;
③过P作PQ∥AC交BG于M,交BO于N,
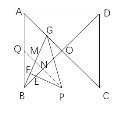
易知三角形ABO为等腰直角三角形,
设OG=x,则AG=![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴△GFP为等腰直角三角形,
同理,设MF=x,结合(1)的结论,
∴![]() ,
,
由(2)得,![]() ,
,
∴![]() ,
,
故③正确;
④连接OP,则OP⊥BC,
由(2)(3)可知,![]() 被均等分为四份,
被均等分为四份,
∴![]() ,
,
由(1)可知,![]() ,
,
∵![]() ,
,![]() ,
,
∴△BEF∽△BGO,
∴![]() ,
,
∵![]() ,
,
∴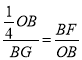
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴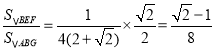 ,
,
故④错误;
故选:A.


科目:初中数学 来源: 题型:
【题目】某单位食堂为全体名职工提供了![]() 四种套餐,为了解职工对这四种套餐的喜好情况,单位随机抽取
四种套餐,为了解职工对这四种套餐的喜好情况,单位随机抽取![]() 名职工进行“你最喜欢哪一种套餐(必选且只选一种)”问卷调查,根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:
名职工进行“你最喜欢哪一种套餐(必选且只选一种)”问卷调查,根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:
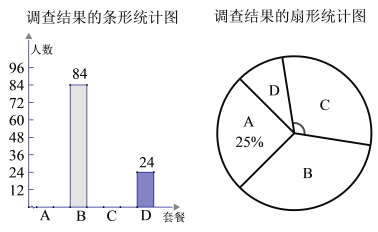
![]() 在抽取的
在抽取的![]() 人中最喜欢
人中最喜欢![]() 套餐的人数为 ,扇形统计图中“
套餐的人数为 ,扇形统计图中“![]() ”对应扇形的圆心角的大小为 ;
”对应扇形的圆心角的大小为 ;
![]() 依据本次调查的结果,估计全体
依据本次调查的结果,估计全体![]() 名职工中最喜欢
名职工中最喜欢![]() 套餐的人数;
套餐的人数;
![]() 现从甲、乙、丙、丁四名职工中任选两人担任“食品安全监督员”,求甲被选到的概率.
现从甲、乙、丙、丁四名职工中任选两人担任“食品安全监督员”,求甲被选到的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,A(t,0),B(t+4,0),线段AB的中点为C,若平面内存在一点P使得∠APC或者∠BPC为直角(点P不与A,B,C重合),则称P为线段AB的直角点.
(1)当t=0时,
①在点P1(![]() ,0),P2(
,0),P2(![]() ,
,![]() ),P3(
),P3(![]() ,﹣
,﹣![]() )中,线段AB的直角点是 ;
)中,线段AB的直角点是 ;
②直线y=![]() x+b上存在四个线段AB的直角点,直接写出b取值范围;
x+b上存在四个线段AB的直角点,直接写出b取值范围;
(2)直线y=![]() x+1与x,y轴交于点M,N.若线段MN上只存在两个线段AB的直角点,直接写出t取值范围.
x+1与x,y轴交于点M,N.若线段MN上只存在两个线段AB的直角点,直接写出t取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 的半径为
的半径为![]() ,
,![]() 的半径为
的半径为![]() ,以
,以![]() 为圆心,以
为圆心,以![]() 的长为半径画弧,再以线段
的长为半径画弧,再以线段![]() 的中点P为圆心,以
的中点P为圆心,以![]() 的长为半径画弧,两弧交于点A,连接
的长为半径画弧,两弧交于点A,连接![]() ,
,![]() ,
,![]() 交
交![]() 于点B,过点B作
于点B,过点B作![]() 的平行线
的平行线![]() 交
交![]() 于点C.
于点C.
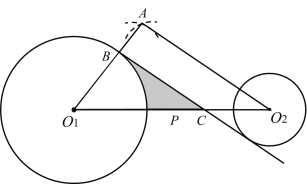
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,
,![]() ,求阴影部分的面积.
,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AB是![]() 的直径,点C是
的直径,点C是![]() 上一点,连接AC、BC,直线MN过点C,满足
上一点,连接AC、BC,直线MN过点C,满足![]() .
.
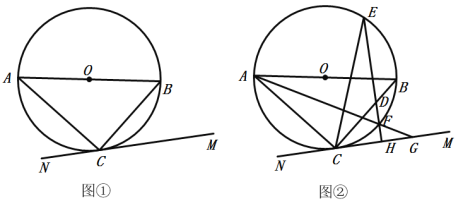
(1)如图①,求证:直线MN是![]() 的切线;
的切线;
(2)如图②,点D在线段BC上,过点D作![]() 于点H,直线DH交
于点H,直线DH交![]() 于点E、F,连接AF并延长交直线MN于点G,连接CE,且
于点E、F,连接AF并延长交直线MN于点G,连接CE,且![]() ,若
,若![]() 的半径为1,
的半径为1,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生社团是指学生在自愿基础上结成的各种群众性文化、艺术、学术团体.不分年级、由兴趣爱好相近的同学组成,在保证学生完成学习任务和不影响学校正常教学秩序的前提下开展各种活动.某校就学生对“篮球社团、动漫社团、文学社团和摄影社团”四个社团选择意向进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整).

请根据图中信息,解答下列问题:
(1)求扇形统计图中m的值,并补全条形统计图;
(2)在“动漫社团”活动中,甲、乙、丙、丁、戊五名同学表现优秀,现决定从这五名同学中任选两名参加“中学生原创动漫大赛”,恰好选中甲、乙两位同学的概率为 .
(3)已知该校有1200名学生,请估计“文学社团”共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:将一个图形绕某一定点按某一方向旋转一定的角度(旋转角度小于等于360°),并且各边长伸缩相同的倍数得到另一个图形,如图①,这种变换叫做旋转伸缩变换,其中定点叫做旋转中心,对应边的比叫做伸缩比.
(特例感知)
(1)如图①,![]() 是等边三角形,
是等边三角形,![]() 绕点A作旋转伸缩变换得
绕点A作旋转伸缩变换得![]() ,连接
,连接![]() ,
,
①若![]() ,则旋转角的度数为________;
,则旋转角的度数为________;
②若伸缩比为2∶1,则线段![]() 的数量关系为________;
的数量关系为________;
③直线![]() 与直线
与直线![]() 所夹的锐角为________;
所夹的锐角为________;
(探究证明)
(2)如图②,在![]() 中,
中,![]() ,将
,将![]() 绕点A逆时针方向旋转一定的角度,作旋转伸缩变换得到
绕点A逆时针方向旋转一定的角度,作旋转伸缩变换得到![]() ,连接
,连接![]() 、
、![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点P,请判断
相交于点P,请判断![]() 的值及
的值及![]() 的度数,并说明理由;
的度数,并说明理由;
(问题解决)
(3)在(2)的条件下,若![]() ,求当点
,求当点![]() 与点P重合时,
与点P重合时,![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老板经营甲、乙两个服装店铺,每个店铺各在同一段时间内都能售出A、B两种款式的服装合计30件且甲店售1件A款和2件B款可获得110元,售2件A和1件B可获得100元,乙店每售出一件A款获得27元,1件B款获利36元,
(1)问在甲店售出1件A和1件B分别获利多少元?
(2)某日王老板进了A款式的服装35件,B款式的服装25件,如果分配给甲店的A款式的服装x件,①求王老板获取的利润y(元)与x(件)之间的函数关系式,并写出x的取值范围;
②由于甲、乙两个店铺所处的地段原因,王老板想在保证乙店利润不小于950元的前提下,使得自己获取的利润最大,请你帮王老板设计一种最佳分配方案,并求最大的总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
某校初二年级的同学乘坐大巴车去北京展览馆参观“砥砺奋进的五年”大型成就展,北京展览馆距离该校12千米,1号车出发3分钟后,2号车才出发,结果两车同时到达,已知2号车的平均速度是1号车的平均速度的1.2倍,求2号车的平均速度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com