
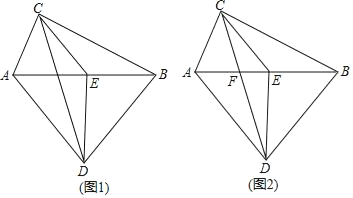
【题目】如图,已知AC⊥BC,AD⊥BD,E为AB的中点,
(1)如图1,求证:△ECD是等腰三角形;
(2)如图2,CD与AB交点为F,若AD=BD,EF=3,DE=4,求CD的长.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1) 求出∠ACB=90°,∠ADB=90°,根据直角三角形定点和底边中点的连线等于底边的一半即可求解.
(2)求出DE⊥AB,再根据相关关系求出△ECD是等腰三角形,可得CD的长.
(1)证明:∵AC⊥BC,AD⊥BD,
∴∠ACB=90°,∠ADB=90°,又∵E为AB的中点,
∴CE=![]() AB,DE=
AB,DE=![]() AB
AB
∴CE=DE,即△ECD是等腰三角形;
(2)∵AD=BD,E为AB的中点,
∴DE⊥AB,
已知DE=4,EF=3,
∴DF=5,
过点E作EH⊥CD,
∵∠FED=90°,EH⊥DF,
∴EH=![]() =
=![]() ,
,
∴DH=![]() =
=![]() ,
,
∵△ECD是等腰三角形,
∴CD=2DH=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠CFE为________度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴相交于A、B两点,点B的坐标为(3,0),与y轴相交于点C(0,﹣3),顶点为D.
(1)求出抛物线y=x2+bx+c的表达式;
(2)连结BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.
①当m为何值时,四边形PEDF为平行四边形.
②设四边形OBFC的面积为S,求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2= ![]() (m为常数,且m≠0)的图象交于点A(﹣2,1)、B(1,n)
(m为常数,且m≠0)的图象交于点A(﹣2,1)、B(1,n) 
(1)求反比例函数与一次函数的解析式;
(2)连接OA、OB,求△AOB的面积;
(3)直接写出当y1<y2时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,需在一面墙上绘制两个形状相同的抛物绒型图案,按照图中的直角坐标系,最高点M到横轴的距离是4米,到纵轴的距离是6米;纵轴上的点A到横轴的距离是1米,右侧抛物线的最大高度是左侧抛物线最大高度的一半.(结果保留整数或分数,参考数据: ![]() =
= ![]() ,
, ![]() =
= ![]() )
) 
(1)求左侧抛物线的表达式;
(2)求右侧抛物线的表达式;
(3)求这个图案在水平方向上的最大跨度是多少米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级举行英语演讲比赛,购买A,B两种笔记本作为奖品,这两种笔记本的单价分别是12元和8元.根据比赛设奖情况,需购买笔记本共30本,并且所购买A笔记本的数量要不多于B笔记本数量的![]() ,但又不少于B笔记本数量
,但又不少于B笔记本数量![]() ,设买A笔记本n本,买两种笔记本的总费为w元.
,设买A笔记本n本,买两种笔记本的总费为w元.
(1)写出w(元)关于n(本)的函数关系式,并求出自变量n的取值范围;
(2)购买这两种笔记本各多少时,费用最少?最少的费用是多少元?
(3)商店为了促销,决定仅对A种类型的笔记本每本让利a元销售,B种类型笔记本售价不变.问购买这两种笔记本各多少本时花费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABE中,∠A=105°,AE的垂直平分线MN交BE于点C,且AB+BC=BE,则∠B的度数是( )

A. 45° B. 60° C. 50° D. 55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为适应日益激烈的市场竞争要求,某工厂从2016年1月且开始限产,并对生产线进行为期5个月的升降改造,改造期间的月利润与时间成反比例;到5月底开始恢复全面生产后,工厂每月的利润都比前一个月增加10万元.设2016年1月为第1个月,第x个月的利润为y万元,其图象如图所示,试解决下列问题: 
(1)分别求该工厂对生产线进行升级改造前后,y与x之间的函数关系式;
(2)到第几个月时,该工厂月利润才能再次达到100万元?
(3)当月利润少于50万元时,为该工厂的资金紧张期,问该工厂资金紧张期共有几个月?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B、C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率;
(2)求三次传球后,球恰在A手中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com