练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．如图，点A的坐标为（-3，0），点B在直线y=-x上运动，连接AB，当线段AB最短时，点B坐标为（-1.5，1.5）．

    分析 垂线段最短，确定B点位置；解直角三角形求解．

    解答 解：作AB⊥直线y=-x于点B．易知△OAB为等腰直角三角形，∠AOB=45°，OA=3．

    作BC⊥x轴于点C，可得OC=$\frac{1}{2}$OA=1.5，BC=OC=1.5．
    ∴当线段AB最短时，点B的坐标为（-1.5，1.5），
    故答案为：（-1.5，1.5）．

    点评 本题考查一次函数问题，关键是根据：垂线段最短以及等腰三角形的底边上的高与中线互相重合．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    16．计算：0.752-$\frac{3}{2}$×$\frac{1}{2}$+0.52=$\frac{1}{16}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．计算：（-$\frac{x}{{3{y^3}}}}$）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．解方程组：$\left\{\begin{array}{l}{2x+y=7}\\{x+2y=8}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．|-$\frac{1}{2017}$|的倒数是（　　）
    A．$\frac{1}{2017}$B．2017C．$-\frac{1}{2017}$D．-2017

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

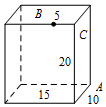    11．长方体的长为15，宽为10，高为20，点B在棱上与点C的距离为5，如图，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，则需要爬行的最短距离是（　　）
    A．$10\sqrt{5}+5$B．$5\sqrt{29}$C．25D．$5\sqrt{37}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

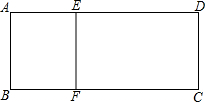    18．如图，在长为15cm，宽为6cm的矩形ABCD中，截去一个矩形ABFE，使得留下的矩形EFCD与截去的矩形ABFE相似，则所截取的线段AE的长度可以是12cm或3cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图，以长方形ABCO中点O为原点，以OC，OA所在直线为x轴和y轴建立平面直角坐标系，点A（0，a），C（b，0）满足$\sqrt{a-2b}$+|b-2|=0．
    （1）求点A，B和C的坐标．
    （2）已知坐标轴上有两动点P，Q同时出发，P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动．Q点从O点出发以2个单位长度每秒的速度沿O→A→B→C的路线移动，点Q到达C点整个运动随之结束．若长方形对角线AC，BO的交点D的坐标是（1，2），设运动时间为t（t＞0）秒．问：是否存在这样的t，使S△ODP=S△ODQ？若存在，请求出t的值；若不存在，请说明理由；
    （3）点F是线段AC上一点，满足∠FOC=∠FCO，点G是第二象限中一点，连OG，使得∠AOG=∠AOF．点E是线段OA上一动点，连CE交OF于点H，下列两个结论：①$\frac{∠OHC-∠ACE}{∠OEC}$的值不变；②$\frac{∠OHC+∠ACE}{∠OEC}$的值不变，其中有且只有一个结论是正确的，请你找出正确的结论并求其值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．某商场将每件进价为20元的玩具以单价为30元的价格出售时，每天可售出300件，经调查当单价每涨1元时，每天少售出10件．若商场想每天获得3750元利润，则每件玩具应涨多少元？这道应用题如果设每件玩具应涨x元，则下列说法错误的是（　　）
    A．涨价后每件玩具的售价是（30+x）元
    B．涨价后每天少售出玩具的数量是10x件
    C．涨价后每天销售玩具的数量是（300-10x）件
    D．可列方程为（30+x）（300-10x）=3750

    查看答案和解析>>

    同步练习册答案