
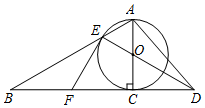
 如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点P为BC的中点,连接EP,AD.
如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点P为BC的中点,连接EP,AD.分析 (1)连接FO,由F为BC的中点,AO=CO,得到OF∥AB,由于AC是⊙O的直径,得出CE⊥AE,根据OF∥AB,得出OF⊥CE,于是得到OF所在直线垂直平分CE,推出FC=FE,OE=OC,再由∠ACB=90°,即可得到结论.
(2)设P点到直线AD的距离为d,记△PAD的面积S△PAD,根据三角形的面积得到d=$\frac{PD•AC}{AD}$ ①由勾股定理得BC=6$\sqrt{3}$,根据平行线的性质得到∠OPC=∠B=30°,推出△OEA为等边三角形,得到∠EOA=60°,在Rt△ACD中,由勾股定理得:AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=3$\sqrt{7}$,将以上数据代入①得即可得到结论.
解答 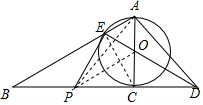 (1)证明:连接CE,如图所示:
(1)证明:连接CE,如图所示:
∵AC为⊙O的直径,
∴∠AEC=90°.
∴∠BEC=90°.
∵点F为BC的中点,
∴EF=BF=CF.
∴∠FEC=∠FCE.
∵OE=OC,
∴∠OEC=∠OCE.
∵∠FCE+∠OCE=∠ACB=90°,
∴∠FEC+∠OEC=∠OEF=90°.
∴EF是⊙O的切线;
(2)解:设P点到直线AD的距离为d,记△PAD的面积S△PAD,
则有:S△PAD=$\frac{1}{2}$AD•d=$\frac{1}{2}$PD•AC,
∴d=$\frac{PD•AC}{AD}$ ①
∵⊙O的半径为3,∠B=30°,
∴∠BAC=60°,AC=6,AB=12,
由勾股定理得BC=6$\sqrt{3}$,
∴PC=3$\sqrt{3}$,
∵O,P分别是AC,BC的中点,
∴OP∥AB,
∴∠OPC=∠B=30°,
∵OE=OA,∠OAE=60°,
∴△OEA为等边三角形,
∴∠EOA=60°,
∴∠ODC=90°-∠COD=90°-∠EOA=30°,
∴∠ODC=∠OPC=30°,
∴OP=OD,
∵OC⊥PD,
∴CD=PC=3$\sqrt{3}$,
在Rt△ACD中,由勾股定理得:AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=3$\sqrt{7}$,
将以上数据代入①得:d=$\frac{PD•AC}{AD}$=$\frac{6\sqrt{3}×6}{3\sqrt{7}}$=$\frac{12\sqrt{21}}{7}$.
点评 本题考查了切线的性质,相似三角形的判定和性质,勾股定理,等边三角形的判定和性质,正确的作出辅助线是解题的关键.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.2×109 | B. | 1.2×108 | C. | 12×109 | D. | 12×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数y=ax2-8ax(a<0)的图象与x轴的正半轴交于点A,它的顶点为P.点C为y轴正半轴上一点,直线AC与该图象的另一交点为B,与过点P且垂直于x轴的直线交于点D,且CB:AB=1:7.
已知二次函数y=ax2-8ax(a<0)的图象与x轴的正半轴交于点A,它的顶点为P.点C为y轴正半轴上一点,直线AC与该图象的另一交点为B,与过点P且垂直于x轴的直线交于点D,且CB:AB=1:7.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
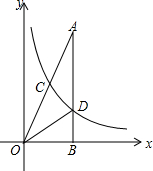 如图,在Rt△AOB中,∠ABO=90°,点B在x轴上,点C(1,a)为OA的中点,反比例函数y=$\frac{k}{x}$的图象经过点C,交AB于点D,且∠AOD=∠BOD,则k=( )
如图,在Rt△AOB中,∠ABO=90°,点B在x轴上,点C(1,a)为OA的中点,反比例函数y=$\frac{k}{x}$的图象经过点C,交AB于点D,且∠AOD=∠BOD,则k=( )| A. | 8 | B. | 2$\sqrt{2}$ | C. | $\sqrt{10}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 问题探究:
问题探究:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com