
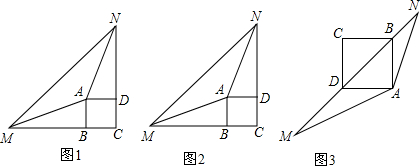
分析 (1)①如图1,先利用SAS证明△ADN≌△ABM,得出AN=AM,∠NAD=∠MAB,再计算出∠NAD=∠MAB=$\frac{1}{2}$(360°-135°-90°)=67.5°.作AE⊥MN于E,根据等腰三角形三线合一的性质得出MN=2NE,∠NAE=$\frac{1}{2}$∠MAN=67.5°.再根据AAS证明△ADN≌△AEN,得出DN=EN,进而得到MN=BM+DN;
②如图2,先利用SAS证明△ABM≌△ADP,得出AM=AP,∠1=∠2=∠3,再计算出∠PAN=360°-∠MAN-(∠3+∠4)=360°-135°-90°=135°.然后根据SAS证明△ANM≌△ANP,得到MN=PN,进而得到MN=BM+DN;
(2)如图3,先由正方形的性质得出∠BDA=∠DBA=45°,根据等角的补角相等得出∠MDA=∠NBA=135°.再证明∠1=∠3.根据两角对应相等的两三角形相似得出△ANB∽△MAD,那么$\frac{BN}{AD}$=$\frac{AB}{MD}$,又AB=AD=$\frac{\sqrt{2}}{2}$DB,变形得出BD2=2BN•MD,然后证明(MD+BD)2+(BD+BN)2=(DM+BD+BN)2,即MB2+DN2=MN2,根据勾股定理的
逆定理即可得出以线段BM,MN,DN的长度为三边长的三角形是直角三角形.
解答 解:(1)①如图1,若BM=DN,则线段MN与BM+DN之间的数量关系是MN=BM+DN.理由如下:
在△ADN与△ABM中,
$\left\{\begin{array}{l}{AD=AB}\\{∠ADN=∠ABM=90°}\\{DN=BM}\end{array}\right.$,
∴△ADN≌△ABM(SAS),
∴AN=AM,∠NAD=∠MAB,
∵∠MAN=135°,∠BAD=90°,
∴∠NAD=∠MAB=$\frac{1}{2}$(360°-135°-90°)=67.5°,
作AE⊥MN于E,则MN=2NE,∠NAE=$\frac{1}{2}$∠MAN=67.5°.
在△ADN与△AEN中,
$\left\{\begin{array}{l}{∠ADN=∠AEN=90°}\\{∠NAD=∠NAE=67.5°}\\{AN=AN}\end{array}\right.$,
∴△ADN≌△AEN(AAS),
∴DN=EN,
∵BM=DN,MN=2EN,
∴MN=BM+DN.
故答案为MN=BM+DN;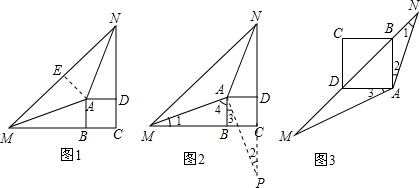 ②如图2,若BM≠DN,①中的数量关系仍成立.理由如下:
②如图2,若BM≠DN,①中的数量关系仍成立.理由如下:
延长NC到点P,使DP=BM,连结AP.
∵四边形ABCD是正方形,
∴AB=AD,∠ABM=∠ADC=90°.
在△ABM与△ADP中,
$\left\{\begin{array}{l}{AB=AD}\\{∠ABM=∠ADP=90°}\\{BM=DP}\end{array}\right.$,
∴△ABM≌△ADP(SAS),
∴AM=AP,∠1=∠2=∠3,
∵∠1+∠4=90°,
∴∠3+∠4=90°,
∵∠MAN=135°,
∴∠PAN=360°-∠MAN-(∠3+∠4)=360°-135°-90°=135°.
在△ANM与△ANP中,
$\left\{\begin{array}{l}{AM=AP}\\{∠MAN=∠PAN=135°}\\{AN=AN}\end{array}\right.$,
∴△ANM≌△ANP(SAS),
∴MN=PN,
∵PN=DP+DN=BM+DN,
∴MN=BM+DN;
(2)如图3,以线段BM,MN,DN的长度为三边长的三角形是直角三角形.理由如下:
∵四边形ABCD是正方形,
∴∠BDA=∠DBA=45°,
∴∠MDA=∠NBA=135°.
∵∠1+∠2=45°,∠2+∠3=45°,
∴∠1=∠3.
在△ANB与△MAD中,
$\left\{\begin{array}{l}{∠ABN=∠MDA=135°}\\{∠1=∠3}\end{array}\right.$,
∴△ANB∽△MAD,
∴$\frac{BN}{AD}$=$\frac{AB}{MD}$,
∴AB2=BN•MD,
∵AB=$\frac{\sqrt{2}}{2}$DB,
∴BN•MD=($\frac{\sqrt{2}}{2}$DB)2=$\frac{1}{2}$BD2,
∴BD2=2BN•MD,
∴MD2+2MD•BD+BD2+BD2+2BD•BN+BN2=MD2+BD2+BN2+2MD•BD+2BD•BN+2BN•MD,
∴(MD+BD)2+(BD+BN)2=(DM+BD+BN)2,
即MB2+DN2=MN2,
∴以线段BM,MN,DN的长度为三边长的三角形是直角三角形.
点评 本题是几何变换综合题,其中涉及到正方形的性质,全等三角形的判定与性质,平行线的性质,等腰三角形的性质,补角的性质,相似三角形的判定与性质,勾股定理的逆定理等知识,综合性较强,有一定难度.准确作出辅助线,利用数形结合是解(1)小题的关键,证明△ANB∽△MAD是解(2)小题的关键.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:填空题
 如图,△ABC的三个顶点都在方格纸的格点上,其中点A的坐标是(-1,0).现将△ABC绕点A顺时针旋转90°,则旋转后点C的坐标是(2,1).
如图,△ABC的三个顶点都在方格纸的格点上,其中点A的坐标是(-1,0).现将△ABC绕点A顺时针旋转90°,则旋转后点C的坐标是(2,1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
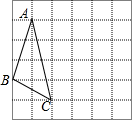 在下面的网格图中,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,已知B,C两点的坐标分别为(-1,-1),(1,-2),将△ABC绕点C顺时针旋转90°,则点A的对应点的坐标为( )
在下面的网格图中,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,已知B,C两点的坐标分别为(-1,-1),(1,-2),将△ABC绕点C顺时针旋转90°,则点A的对应点的坐标为( )| A. | (4,1) | B. | (4,-1) | C. | (5,1) | D. | (5,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我们把两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD,请你写出与筝形ABCD的角或者对角线有关的一个结论,并证明你的结论.
我们把两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD,请你写出与筝形ABCD的角或者对角线有关的一个结论,并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{π}$ | B. | $\frac{4}{π}$ | C. | $\frac{3}{π}$或$\frac{4}{π}$ | D. | $\frac{6}{π}$或$\frac{8}{π}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
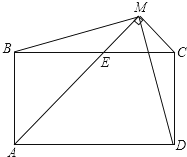 如图,已知矩形ABCD中,过点C引∠A的平分线AM的垂线,垂足为M,AM交BC于E,连接MB,MD.
如图,已知矩形ABCD中,过点C引∠A的平分线AM的垂线,垂足为M,AM交BC于E,连接MB,MD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
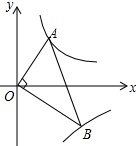 如图,第一角限内的点A在反比例函数$y=\frac{2}{x}$的图象上,第四象限内的点B 在反比例函数$y=\frac{k}{x}$图象上,且OA⊥OB,∠OAB=60度,则k值为-6.
如图,第一角限内的点A在反比例函数$y=\frac{2}{x}$的图象上,第四象限内的点B 在反比例函数$y=\frac{k}{x}$图象上,且OA⊥OB,∠OAB=60度,则k值为-6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com