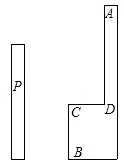
解:连接PA、PB,过点P作PM⊥AD于点M,延长BC,交PM于点N。

则∠APM=45°,∠BPM=60°,NM=10米。
设PM=x米
在Rt△PMA中,AM=PM×tan∠APM=xtan45°=x,
在Rt△PNB中,BN=PN×tan∠BPM=(x-10)tan60°=
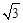
(x-10),
由AM+BN=46米,得x +
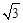
( x-10)=46,
解得,
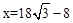
。
∴点P到AD的距离为
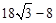
米。
连接PA、PB,过点P作PM⊥AD于点M;延长BC,交PM于点N,将实际问题中的已知量转化为直角三角形中的有关量,设PM=x米,在Rt△PMA中,表示出AM,在Rt△PNB中,表示出BN,由AM+BN=46米列出方程求解即可。

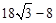 米
米
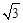 (x-10),
(x-10),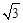 ( x-10)=46,
( x-10)=46,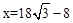 。
。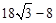 米。
米。 
