
【题目】已知如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.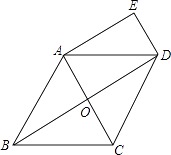
(1)求证:四边形AODE是矩形;
(2)若AB=6,∠BCD=120°,求四边形AODE的面积.
【答案】
(1)证明:∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵在菱形ABCD中,AC⊥BD,
∴∠AOD=90°,
∴四边形AODE是矩形;
(2)解:∵∠BCD=120°,AB∥CD,
∴∠ABC=180°﹣120°=60°,
∵AB=BC,
∴△ABC是等边三角形,
∴OA= ![]() ×6=3,OB=
×6=3,OB= ![]() ×6=3
×6=3 ![]() ,
,
∵四边形ABCD是菱形,
∴OD=OB=3 ![]() ,
,
∴四边形AODE的面积=OAOD=3×3 ![]() =9
=9 ![]() .
.
【解析】(1)由已知DE∥AC,AE∥BD,可证得四边形AODE是平行四边形,再证明有一个角是直角,由菱形ABCD,即可证出∠AOD是直角,即可证得结论。
(2)抓住已知∠BCD=120°,根据菱形的性质证明△ABC是等边三角形,再利用勾股定理求出OA、OD的长,即可求出矩形AODE的面积。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断

A.甲正确,乙错误 B.乙正确,甲错误 C.甲、乙均正确 D.甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E,∠ABC、∠BCD的角平分线交于点F.
(1)若∠F=70°,则∠ABC+∠BCD= ______ °;∠E= ______ °;
(2)探索∠E与∠F有怎样的数量关系,并说明理由;
(3)给四边形ABCD添加一个条件,使得∠E=∠F,所添加的条件为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形![]() 的三个项点坐标为:
的三个项点坐标为:![]() △
△![]() 内有一点
内有一点![]() 经过平移后的对应点为
经过平移后的对应点为![]() ,将△
,将△![]() 做同样平移得到△
做同样平移得到△![]() .
.

(1)写出![]() 三点的坐标:;
三点的坐标:;
(2)在图中画出△![]() ;
;
(3)求出△![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分) 小丽想用一块面积为400cm2的正方形纸片,沿着边的方向裁处一块面积为300cm2的长方形纸片.(1)请帮小丽设计一种可行的裁剪方案;
(2)若使长方形的长宽之比为3:2,小丽能用这块纸片裁处符合要求的纸片吗?若能,请帮小丽设计一种裁剪方案,若不能,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线 ![]() 分别与x轴、y轴交于点B、C,且与直线
分别与x轴、y轴交于点B、C,且与直线 ![]() 交于点A.
交于点A.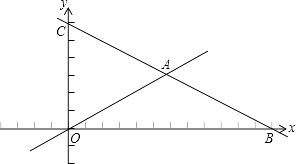
(1)分别求出点A、B、C的坐标;
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的函数表达式;
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com