
| t | x |
 曲线为C2,直线l1:y=kx+b(k、b为常数,k≠0)与双曲线C2的交点分别为A(1,m),B(n,-1).
曲线为C2,直线l1:y=kx+b(k、b为常数,k≠0)与双曲线C2的交点分别为A(1,m),B(n,-1).| k |
| x |
| 4 |
| x |
| 4 |
| x |

|
|


科目:初中数学 来源: 题型:
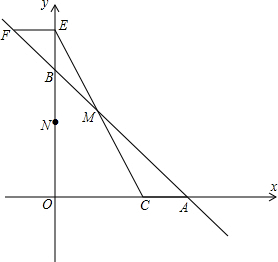 明理由.②若C2、C3中的y都随着x的增大而减小,写出x的取值范围.
明理由.②若C2、C3中的y都随着x的增大而减小,写出x的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:
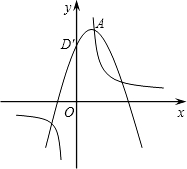 、F四点组成的四边形的面积为16.5时,先求出P点坐标,并在直线y=x上求一点M,使|MD-MP|的值最大.
、F四点组成的四边形的面积为16.5时,先求出P点坐标,并在直线y=x上求一点M,使|MD-MP|的值最大.查看答案和解析>>
科目:初中数学 来源: 题型:
6
| ||
| x |
| 2 |
3
| ||
| 2 |
| 2 |
3
| ||
| 2 |
6
| ||
| x |
6
| ||
| x |
查看答案和解析>>
科目:初中数学 来源:北京期末题 题型:解答题
 (t为常数,t≠0)经过点M(-2,2);它关于y轴对称的双曲线为C2, 直线
(t为常数,t≠0)经过点M(-2,2);它关于y轴对称的双曲线为C2, 直线 :
: (k、b为常数,k≠0)与双曲线的交点分别为A(1,m),B(n,-1 )
(k、b为常数,k≠0)与双曲线的交点分别为A(1,m),B(n,-1 ) 的解析式;
的解析式; 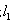 的解析式;
的解析式;  平移后得到的直线
平移后得到的直线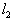 与双曲线
与双曲线 的交点分别记为C、D(A和D,B和C分别在双曲线
的交点分别记为C、D(A和D,B和C分别在双曲线 的同一支上),四边形ABCD恰好为矩形,请直接写出直线CD的解析式。
的同一支上),四边形ABCD恰好为矩形,请直接写出直线CD的解析式。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com