
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)写出点B的坐标;
(3)将△ABC向右平移5个单位长度,向下平移2个单位长度,画出平移后的图形△A′B′C′;
(4)计算△A′B′C′的面积﹒
(5)在x轴上存在一点P,使PA+PC最小,直接写出点P的坐标.

【答案】(1)详见解析;(2)B(-2,1);(3)详见解析;(4)4;(5)P(![]() ,0).
,0).
【解析】
(1)直接利用已知点位置得出x,y轴的位置;
(2)利用平面直角坐标系得出B点坐标即可;
(3)直接利用平移的性质得出对应点位置进而得出答案;
(4)利用△A′B′C′所在矩形形面积减去周围三角形面积进而得出答案.
(5)作C关于x轴的对称点D,连接AD交x轴一点就为所求点.
(1)如图所示,∵点A的坐标为(﹣4,5),
∴在A点y轴向右平移4个单位,x轴向下平移5个单位得到即可;

(2)B(﹣2,1);
(3)如图所示:△A′B′C′即为所求;

(4)△A′B′C′的面积为:3×4﹣![]() ×3×2﹣
×3×2﹣![]() ×1×2﹣
×1×2﹣![]() ×2×4=4.
×2×4=4.
(5)作点C关于x轴的对称点D(-1,-3),连接AD交x轴于一点,该点为所求点.
设直线AD:y=kx+b,将A(-4,5),D(-1,-3)代入
![]() 解得:
解得:
直线AD:![]()
令y=0,则x=![]()
∴P点坐标为(![]() ,0)
,0)



科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上,以AD为折痕将△ABD折叠得到△AB′D,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是_______.
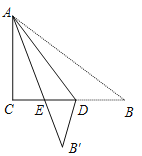
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分9分)
根据要求,解答下列问题.
(1)根据要求,解答下列问题.
①方程x2-2x+1=0的解为________________________;
②方程x2-3x+2=0的解为________________________;
③方程x2-4x+3=0的解为________________________;
…… ……
(2)根据以上方程特征及其解的特征,请猜想:
①方程x2-9x+8=0的解为________________________;
②关于x的方程________________________的解为x1=1,x2=n.
(3)请用配方法解方程x2-9x+8=0,以验证猜想结论的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三个登山爱好者经常相约去登山,今年1月甲参加了两次登山活动.
(1)1月1日甲与乙同时开始攀登一座900米高的山,甲的平均攀登速度是乙的1.2倍,结果甲比乙早15分钟到达顶峰.求甲的平均攀登速度是每分钟多少米?
(2)1月6日甲与丙去攀登另一座h米高的山,甲保持第(1)问中的速度不变,比丙晚出发0.5小时,结果两人同时到达顶峰,问甲的平均攀登速度是丙的多少倍?(用含h的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程,解应用题
甲乙两人相约周末到影院看电影,他们的家分别距离影院1200米和2000米,两人分别从家中同时出发,已知甲和乙的速度比是![]() ,结果甲比乙提前4分钟到达影院.
,结果甲比乙提前4分钟到达影院.
(1)求甲、乙两人的速度?
(2)在看电影时,甲突然接到家长电话让其15分钟内赶回家,时间紧迫改变速度,比来时每分钟多走25米,甲是否能按要求时间到家?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长春市对全市各类(A型、B型、C型.其它型)校车共848辆进行环保达标普查,普查结果绘制成如下条形统计图:
(1)求全市各类环保不达标校车的总数;
(2)求全市848辆校车中环保不达标校车的百分比;
(3)规定环保不达标校车必须进行维修,费用为:A型500元/辆,B型1000元/辆,C型600元/辆,其它型300元/辆,求全市需要进行维修的环保不达标校车维修费的总和;
(4)若每辆校车乘坐40名学生,那么一次性维修全部不达标校车将会影响全市80000名学生乘校车上学的百分比是

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,给出如下定义:已知两个函数,如果对于任意的自变量x,这两个函数对应的函数值记为y1、y2,都有点(x,y1)和(x,y2)关于点(x,x)中心对称(包括三个点重合时),由于对称中心都在直线y=x上,所以称这两个函数为关于直线y=x的特别对称函数.例如:y=![]() x和y=
x和y=![]() 为关于直线y=x的特别对称函数.
为关于直线y=x的特别对称函数.
(1)若y=3x+2和y=kx+t(k≠0)为关于直线y=x的特别对称函数,点M(1,m)是y=3x+2上一点.
①点M(1,m)关于点(1,1)中心对称的点坐标为 .
②求k、t的值.
(2)若y=3x+n和它的特别对称函数的图象与y轴围成的三角形面积为2,求n的值.
(3)若二次函数y=ax2+bx+c和y=x2+d为关于直线y=x的特别对称函数.
①直接写出a、b的值.
②已知点P(﹣3,1)、点Q(2,1),连结PQ,直接写出y=ax2+bx+c和y=x2+d两条抛物线与线段PQ恰好有两个交点时d的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的情景对话,然后解答问题:
老师:我们定义一种三角形,两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.
小华:等边三角形一定是奇异三角形!
小明:那直角三角形中是否存在奇异三角形呢?
问题(1):根据“奇异三角形”的定义,请你判断小华提出的猜想:“等边三角形一定是奇异三角形”是否正确?__________.(填“是”或“否”)
问题(2):已知RtΔABC中,两边长分别是![]() ,10,,若这个三角形是奇异三角形,则第三边是__________.
,10,,若这个三角形是奇异三角形,则第三边是__________.
问题(3):如图,以AB为斜边分别在AB的两侧作直角三角形,且AD=BD,若四边形ADBC内存在点E,使得AE=AD,CB=CE.试说明:△ACE是奇异三角形.
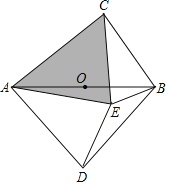
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com