
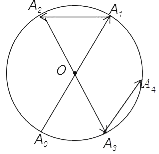
【题目】如图所示,一动点从半径为2的⊙O上的A0点出发,沿着射线A0O方向运动到⊙O上的点A1处,再向左沿着与射线A1O夹角为60°的方向运动到⊙O上的点A2处;接着又从A2点出发,沿着射线A2O方向运动到⊙O上的点A3处,再向左沿着与射线A3O夹角为60°的方向运动到⊙O上的点A4处;A4A0间的距离是_____;…按此规律运动到点A2019处,则点A2019与点A0间的距离是_____.
科目:初中数学 来源: 题型:
【题目】从﹣2,﹣![]() ,0,4中任取一个数记为m,再从余下的三个数中,任取一个数记为n,若k=mn.
,0,4中任取一个数记为m,再从余下的三个数中,任取一个数记为n,若k=mn.
(1)请用列表或画树状图的方法表示取出数字的所有结果;
(2)求正比例函数y=kx的图象经过第一、三象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A,对点A作如下变换:
第一步:作点A关于x轴的对称点A1;第二步:以O为位似中心,作线段OA1的位似图形OA2,且相似比![]() =q,则称A2是点A的对称位似点.
=q,则称A2是点A的对称位似点.
(1)若A(2,3),q=2,直接写出点A的对称位似点的坐标;
(2)已知直线l:y=kx-2,抛物线C:y=-![]() x2+mx-2(m>0).点N(
x2+mx-2(m>0).点N(![]() ,2k-2)在直线l上.
,2k-2)在直线l上.
①当k=![]() 时,判断E(1,-1)是否是点N的对称位似点,请说明理由;
时,判断E(1,-1)是否是点N的对称位似点,请说明理由;
②若直线l与抛物线C交于点M(x1,y1)(x1≠0),且点M不是抛物线的顶点,则点M的对称位似点是否可能仍在抛物线C上?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3.动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒(0<x<4)时,解答下列问题:
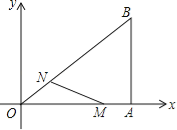
(1)求点N的坐标(用含x的代数式表示);
(2)设△OMN的面积是S,求S与x之间的函数表达式;当x为何值时,S有最大值?最大值是多少?
(3)在两个动点运动过程中,是否存在某一时刻,使△OMN是直角三角形?若存在,求出x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用同样规格黑白两色的正方形瓷砖铺设长方形地面,请观察下列图形,并解答有关问题:

(1)在第n个图中,第一横行共 块瓷砖,第一竖列共有 块瓷砖;(均用含n的代数式表示)铺设地面所用瓷砖的总块数为 (用含n的代数式表示,n表示第n个图形)
(2)上述铺设方案,铺一块这样的长方形地面共用了506块瓷砖,求此时n的值;
(3)是否存在黑瓷砖与白瓷砖块数相等的情形?请通过计算加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() .
.
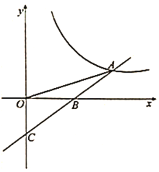
(1)求反比例函数与一次函数的表达式;
(2)若点![]() 为x轴上一点,
为x轴上一点,![]() 是等腰三角形,求点
是等腰三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着2019年全国两会的隆重召开,中学生对时事新闻的关注空前高涨,某校为了解中学生对时事新闻的关注情况,组织全校九年级学生开展“时事新闻大比拼”比赛,随机抽取九年级的25名学生的成绩(满分为100分)整理统计如下:收集数据 25名学生的成绩(满分为100分)统计如下(单位:分)
90 ,74 ,88 ,65 ,98 ,75 , 81 ,44 ,85 ,70 ,55 , 80 , 95 ,88 ,72 ,87 , 60 ,56 ,76 ,66 ,78 ,72 ,82 ,63 ,100
整理数据:按如下分组整理样本数据并补全表格:
成绩 | 90≤ | 75≤ | 60≤ |
|
人数 | 10 | 8 |
分析数据 补充完成下面的统计分析表:
平均数 | 中位数 | 方差 |
76 | 190. 88 |
得出结论:
(1)若全校九年级有1000名学生,请估计全校九年级有多少学生成绩达到90分及以上;
(2)若八年级的平均数为76分,中位数为80分,方差为102. 5,请你分别从平均数、中位数和方差三个方面做出评价,你认为哪个年级的成绩较好?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,过AB边上点D作DG∥BC,交AC于点G,在GD的延长线上取点E,使ED=CG,连接AE,CD.

(1)求证:AE=DC;
(2)过E作EF∥DC,交BC于点F,求证:∠AEF=∠ACB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com