
【题目】在直角坐标系中,有如图所示的Rt△ABO,AB⊥x轴于点B,斜边AO=10,直角边AB=6,反比例函数y= ![]() (x>0)的图象经过AO的中点C,且与AB交于点D,则点D的坐标为 .
(x>0)的图象经过AO的中点C,且与AB交于点D,则点D的坐标为 . 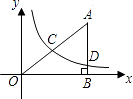
【答案】(8,1.5)
【解析】解:过C点作CE⊥OB于E, ∵AB⊥OB,CE⊥OB,
∴CE∥AB,又C为OA的中点,
∴E为OB的中点,即CE为△AOB的中位线,
∴CE= ![]() AB,OE=
AB,OE= ![]() OB,
OB,
在Rt△AOB中,AO=10,AB=6,
根据勾股定理得:OB= ![]() =8,
=8,
∴OE=4,CE=3,
∴C的坐标是(4,3),
将C(4,3)代入y= ![]() 中得:k=12,
中得:k=12,
则反比例函数解析式为y= ![]() ;
;
∵AB⊥x轴,D在AB上,且OB=8,
∴点D的横坐标为8,
将x=8代入y= ![]() 中得:y=1.5,
中得:y=1.5,
∴点D的坐标为(8,1.5).
故答案是:(8,1.5).
过C作x轴的垂线,垂足为点E,由AB也与x轴垂直,得到CE与AB平行,又C为OA的中点,可得出E为OB的中点,即CE为三角形AOB的中位线,在直角三角形AOB中,根据斜边AO的长及sin∠AOB的值,利用锐角三角函数定义求出AB的长,再利用勾股定理求出OB的长,利用三角形中位线定理得到CE等于AB的一半,可得出CE的长,即为C的纵坐标,由OE等于OB的一半,由OB的长求出OE的长,即为点C的横坐标,确定出点C的坐标,将点C的坐标代入到y= ![]() 中,求出k的值,即可确定出反比例函数解析式;由AB与x轴垂直,且D在AB上,可得出D与B的横坐标相同,由OB的长得出D的横坐标,将求出的D的横坐标代入反比例函数解析式中,求出对应的y的值,即为D的纵坐标,即可确定出D的坐标.
中,求出k的值,即可确定出反比例函数解析式;由AB与x轴垂直,且D在AB上,可得出D与B的横坐标相同,由OB的长得出D的横坐标,将求出的D的横坐标代入反比例函数解析式中,求出对应的y的值,即为D的纵坐标,即可确定出D的坐标.


科目:初中数学 来源: 题型:
【题目】某同学对数据26,36,36,46,5■,52进行统计分析发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )
A.平均数B.中位数C.方差D.众数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少?”共有4个选题.
A.1.5小时以上 B.1~1.5小时 C.0.5~1小时 D.0.5小时以下
请你根据统计图提供的信息,解答以下问题:
(1)本次一共调查了多少名学生?
(2)将条形统计图选项B补充完整;
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下?
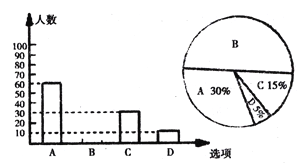
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面某校八年级师生的对话内容,再解答问题.(温馨提示:一周只上五天课,另外考试时每半天考一科)
小明:“听说下周会进行连续两天的期中考试.”
刘老师:“是的,要考语文、数学、英语、物理共四科,但具体星期几不清楚.”
小宇:“我估计是星期四、星期五.”
(1)求小宇猜对的概率;
(2)若考试已定在星期四、星期五进行,但各科考试顺序没定,请用恰当的方法求同一天考语文、数学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=k1x+b(k1≠0)与双曲线y= ![]() (k2≠0)相交于A(1,m)、B(﹣2,﹣1)两点.
(k2≠0)相交于A(1,m)、B(﹣2,﹣1)两点. 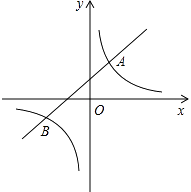
(1)求直线和双曲线的解析式.
(2)若A1(x1 , y1),A2(x2 , y2),A3(x3 , y3)为双曲线上的三点,且x1<x2<0<x3 , 请直接写出y1 , y2 , y3的大小关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以线段AC为对角线的凸四边形ABCD(它的四个顶点A、B、C、D按顺时针方向排列,每个内角均小于180°),已知AB=BC=CD,∠ABC=120°,∠CAD=30°,则∠BCD的大小为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com