
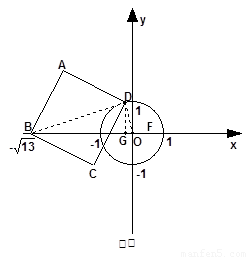
已知⊙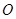 的半径为1,以
的半径为1,以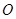 为原点,建立如图所示的直角坐标系.有一个正方形
为原点,建立如图所示的直角坐标系.有一个正方形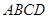 ,顶点
,顶点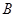 的坐标为(
的坐标为(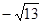 ,0),顶点
,0),顶点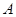 在
在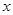 轴上方,顶点
轴上方,顶点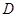 在⊙
在⊙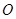 上运动.
上运动.
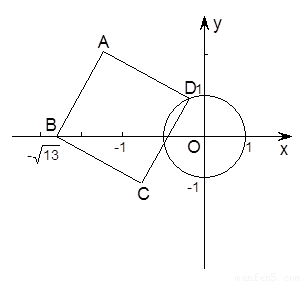
(1)当点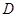 运动到与点
运动到与点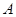 、
、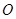 在一条直线上时,
在一条直线上时,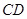 与⊙
与⊙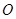 相切吗?如果相切,请说明理由,并求出
相切吗?如果相切,请说明理由,并求出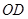 所在直线对应的函数表达式;如果不相切,也请说明理由;
所在直线对应的函数表达式;如果不相切,也请说明理由;
(2)设点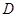 的横坐标为
的横坐标为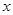 ,正方形
,正方形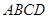 的面积为
的面积为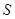 ,求出
,求出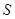 与
与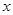 的函数关系式,并求出
的函数关系式,并求出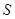 的最大值和最小值.
的最大值和最小值.
(1)CD与⊙O相切,y=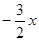 (2)S
(2)S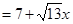 ,S的最大值为
,S的最大值为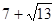 ,S的最小值为
,S的最小值为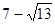
【解析】(1)CD与⊙O相切。 1分
因为A、D、O在一直线上,∠ADC=90°,
所以∠COD=90°,所以CD是⊙O的切线 3分
CD与⊙O相切时,有两种情况:①切点在第二象限时(如图①),
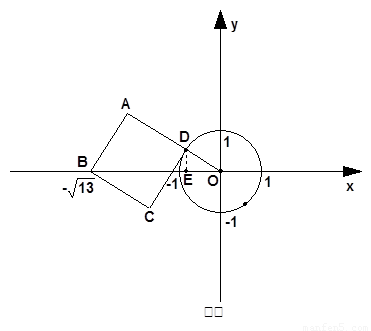
设正方形ABCD的边长为a,则a2+(a+1)2=13,
解得a=2,或a=-3(舍去) 4分
过点D作DE⊥OB于E,则Rt△ODE≌Rt△OBA,所以 ,所以DE=
,所以DE=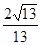 ,
,
OE= ,所以点D1的坐标是(-
,所以点D1的坐标是(- ,
,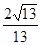 )
5分
)
5分
所以OD所在直线对应的函数表达式为y=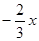 6分
6分
②切点在第四象限时(如图②),
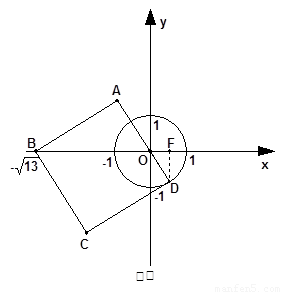
设正方形ABCD的边长为b,则b2+(b-1)2=13,
解得b=-2(舍去),或b=3 7分
过点D作DF⊥OB于F,则Rt△ODF∽Rt△OBA,所以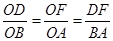 ,所以OF=
,所以OF=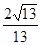 ,DF=
,DF= ,所以点D2的坐标是(
,所以点D2的坐标是(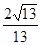 ,-
,- )
8分
)
8分
所以OD所在直线对应的函数表达式为y=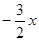 9分
9分
(2)如图③,
过点D作DG⊥OB于G,连接BD、OD,则BD2=BG2+DG2=(BO-OG)2+OD2-OG2=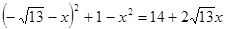 10分
10分
所以S=AB2=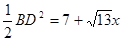 11分
11分
因为-1≤x≤1,所以S的最大值为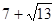 ,
,
S的最小值为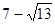 12分
12分
(1)易证CD是⊙O的切线,根据Rt△ODE∽Rt△OBA得到DE的长,再求出D1的坐标,根据待定系数法,求出函数解析式;
(2)过点D作DG⊥OB于G,连接BD、OD,则BD2=BG2+DG2=(BO-OG)2+OD2-OG2,所以S=AB2=  BD2=7+
BD2=7+ 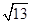 x,因为-1≤x≤1,所以S的最大值就可以求出.
x,因为-1≤x≤1,所以S的最大值就可以求出.


科目:初中数学 来源: 题型:
 |
| AB |
 点A、点B重合).连接AC、BC,分别与⊙M相交于点D、点E,连接DE.若AB=2
点A、点B重合).连接AC、BC,分别与⊙M相交于点D、点E,连接DE.若AB=2| 3 |
| AD |
| DC |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知⊙O的半径为1,以O为原点,建立如图所示的直角坐标系.有一个正方形ABCD,顶点B的坐标为(-
已知⊙O的半径为1,以O为原点,建立如图所示的直角坐标系.有一个正方形ABCD,顶点B的坐标为(-| 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 |
| AOB |
 |
| BCA |
| ||
| 2 |
| ||
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com