
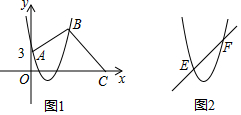
���� ��1�����ô���ϵ�������ɽ�����⣮
��2���������ֱ��AB��BC�Ľ���ʽ���ɽ�����⣮
��3���������ߵĽ���ʽΪy=x2-4x+3�Ķ������꣨2��-1��������Ϊ��������y=x2+bx+c����ƽ��2����λ���ȣ�������ƽ��1����λ���ȣ��õ����µ������ߵĽ���ʽΪy=x2������ͼ��ʾ������EF��y�ύ�ڵ�C����OC=2�����������ε������ʽ�г����̼��ɽ�����⣮
��� �⣺��1���ѵ�A��0��3����B��5��8�����������y=x2+bx+c�У��õ�$\left\{\begin{array}{l}{c=3}\\{25+5b+c=8}\end{array}\right.$��
���$\left\{\begin{array}{l}{b=-4}\\{c=3}\end{array}\right.$��
�������ߵĽ���ʽΪy=x2-4x+3��
��2����A��0��3����B��5��8������ֱ��AB�Ľ���ʽΪy=mx+n������$\left\{\begin{array}{l}{n=3}\\{5m+n=8}\end{array}\right.$��
���$\left\{\begin{array}{l}{m=1}\\{n=3}\end{array}\right.$��
��ֱ��AB�Ľ���ʽΪy=x+3��
�ߡ�ABC=90�㣬
��BC��AB����ֱ��BC�Ľ���ʽΪy=-x+b�䣬�ѣ�5��8������õ�b��=13��
��ֱ��BC�Ľ���ʽΪy=-x+13����y=0����x=13��
��C��13��0����
��3���������ߵĽ���ʽΪy=x2-4x+3�Ķ������꣨2��-1����
�ཫ������y=x2+bx+c����ƽ��2����λ���ȣ�������ƽ��1����λ���ȣ�
�õ����µ������ߵĽ���ʽΪy=x2������ͼ��ʾ������EF��y�ύ�ڵ�C����OC=2��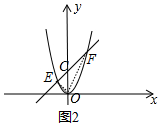
��$\left\{\begin{array}{l}{y=kx+2}\\{y={x}^{2}}\end{array}\right.$����ȥy�õ�x2-kx-2=0��
��x1+x2=k��x1x2=-2��
��x2-x1=$\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{{k}^{2}+8}$��
��S��EOF=$\frac{1}{2}$•OC•��x2-x1����
��3=$\frac{1}{2}$•2•$\sqrt{{k}^{2}+8}$��
��k2=1��
��k��0��
��k=1��
���� ���⿼����κ����ۺ��⡢����ϵ��������ֱ�ߴ�ֱ�������������ε������ʽ��һԪ���η��̵ĸ���ϵ���Ĺ�ϵ��֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ���÷��̵�˼��˼�����⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У�����OABC�Ķ���A��C������ֱ�Ϊ��9��0������0��4������D������Ϊ��5��0������P�ؾ��εı�C-B-A-O-C�˶�������ODP������Ϊ5�ĵ���������ʱ����P������Ϊ��3��4������2��4������8��4������9��3����
��ͼ����ƽ��ֱ������ϵ�У�����OABC�Ķ���A��C������ֱ�Ϊ��9��0������0��4������D������Ϊ��5��0������P�ؾ��εı�C-B-A-O-C�˶�������ODP������Ϊ5�ĵ���������ʱ����P������Ϊ��3��4������2��4������8��4������9��3�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
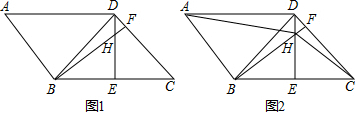
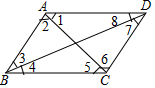 ��ͼ����AD��BC�����1=��5����8=��4����ABC+��BAC=180�㣻��DC��AB�����3=��7����2=��6����ABC+��BCD=180��
��ͼ����AD��BC�����1=��5����8=��4����ABC+��BAC=180�㣻��DC��AB�����3=��7����2=��6����ABC+��BCD=180���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
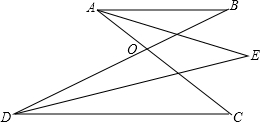 ��ͼ��AB��CD��AC��BD���ڵ�O����A����D�Ľ�ƽ���߽��ڵ�E����֪��E=50�㣬���AOB�Ķ�����
��ͼ��AB��CD��AC��BD���ڵ�O����A����D�Ľ�ƽ���߽��ڵ�E����֪��E=50�㣬���AOB�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com