
 如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12,EF=16,则边AB的长是( )
如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12,EF=16,则边AB的长是( )| A. | 8+6$\sqrt{3}$ | B. | 12$\sqrt{3}$ | C. | 19.2 | D. | 20 |
分析 利用翻折变换的性质得出四边形EFGH是矩形,进而得出BF=DH=MF,再利用勾股定理得出BE,BF的长,进而得出答案.
解答 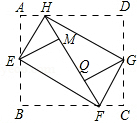 解:如图所示:设HF上两个点分别为M、Q,
解:如图所示:设HF上两个点分别为M、Q,
∵M点是B点对折过去的,
∴∠EMH为直角,△AEH≌△MEH,
∴∠HEA=∠MEH,
同理∠MEF=∠BEF,
∴∠MEH+∠MEF=90°,
∴四边形EFGH是矩形,
∴△DHG≌△BFE,△HEF是直角三角形,
∴BF=DH=MF,
∵AH=HM,
∴AD=HF,
∵EH=12,EF=16,
∴FH=$\sqrt{E{H}^{2}+E{F}^{2}}$=$\sqrt{1{2}^{2}+1{6}^{2}}$=20,
∴AE=EM=$\frac{EH×EF}{FH}$=$\frac{12×16}{20}$=$\frac{48}{5}$,
则BF=NF=$\sqrt{E{F}^{2}-E{M}^{2}}$=12.8,
故BE=$\sqrt{E{F}^{2}-B{F}^{2}}$=9.6,
∴AB=AE+BE=9.6+$\frac{48}{5}$=19.2.
故选:C.
点评 此题主要考查了翻折变换的性质以及勾股定理、矩形的判定方法等知识,根据题意得出AE,BE的长是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察k1,k2,k3的大小关系为( )
如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察k1,k2,k3的大小关系为( )| A. | k1>k2>k3 | B. | k2>k3>k1 | C. | k3>k2>k1 | D. | k3>k1>k2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+4)(a-4)=a2-4 | B. | (5x-1)(1-5x)=25x2-1 | ||
| C. | (-3x+2)2=4-12x+9x2 | D. | (x-3)(x-9)=x2-27 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com