
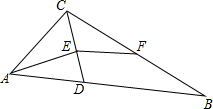
 如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足为E,F是BC中点,探究BD与EF的关系.并说明理由.
如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足为E,F是BC中点,探究BD与EF的关系.并说明理由.科目:初中数学 来源: 题型:
 甲、乙两名自行车爱好者准备在一段长为3500米的笔直公路上进行比赛,比赛开始时乙在起点,甲在乙的前面.他们同时出发,匀速前进,已知甲的速度为12米/秒,设甲、乙两人之间的距离为s(米),比赛时间为t(秒),图中的折线表示从两人出发至其中一人先到达终点的过程中s(米)与t(秒)的函数关系.根据图中信息,回答下列问题:
甲、乙两名自行车爱好者准备在一段长为3500米的笔直公路上进行比赛,比赛开始时乙在起点,甲在乙的前面.他们同时出发,匀速前进,已知甲的速度为12米/秒,设甲、乙两人之间的距离为s(米),比赛时间为t(秒),图中的折线表示从两人出发至其中一人先到达终点的过程中s(米)与t(秒)的函数关系.根据图中信息,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com