
【题目】已知:AB为⊙O的直径.
(1)作OB的垂直平分线CD,交⊙O于C、D两点;
(2)在(1)的条件下,连接AC、AD,则△ACD为 三角形.
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.

(1)求反比例函数和一次函数的解析式;
(2)根据图象写出一次函数的值大于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,点E是平面内异于点A的任意一点,以线段AE为边作正方形AEFG,连接EB,GD.
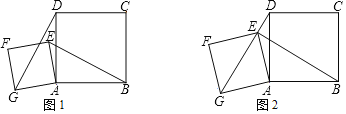
(1)如图1,求证EB=GD;
(2)如图2,若点E在线段DG上,AB=5,AG=3![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB,
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求出经过点E的反比例函数解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=![]() x2+bx+c与x轴交于A(4,0)、B(﹣2,0),与y轴交于点C.
x2+bx+c与x轴交于A(4,0)、B(﹣2,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)点D为第四象限抛物线上一点,设点D的横坐标为m,四边形ABCD的面积为S,求S与m的函数关系式,并求S的最值;
(3)点P在抛物线的对称轴上,且∠BPC=45°,请直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,平行四边形ABOC的顶点B,C在反比例函数y=![]() (x>O)的图象上,点A在反比例函数y=
(x>O)的图象上,点A在反比例函数y=![]() (k>O)的图象上,若点B的坐标为(1,2),∠OBC=90°,则k的值为( )
(k>O)的图象上,若点B的坐标为(1,2),∠OBC=90°,则k的值为( )
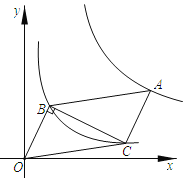
A.![]() B.3 C.5 D.12.5
B.3 C.5 D.12.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”倡议提出五年多来,交通、通信、能源等各项相关建设取得积极进展,也为增进各国民众福祉提供了新的发展机遇.下图是2017年“一年一路”沿线部分国家的通信设施现状统计图.
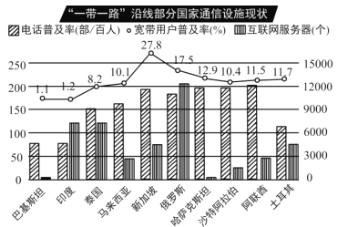
根据统计图提供的信息,下列推断合理的是( ).
A.互联网服务器拥有个数最多的国家是阿联酋
B.宽带用户普及率的中位数是11.05%
C.有8个国家的电话普及率能够达到平均每人1部
D.只有俄罗斯的三项指标均超过了相应的中位数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线y=x2-2mx-3m
(1)当m=1时,
①抛物线的对称轴为直线______,
②抛物线上一点P到x轴的距离为4,求点P的坐标
③当n≤x≤![]() 时,函数值y的取值范围是-
时,函数值y的取值范围是-![]() ≤y≤2-n,求n的值
≤y≤2-n,求n的值
(2)设抛物线y=x2-2mx-3m在2m-1≤x≤2m+1上最低点的纵坐标为y0,直接写出y0与m之间的函数关系式及m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com