Question

1．【已知】在Rt△ABC中，∠C=90°，BC=3，AC=4，P为AC边上的一动点．
操作：请在图1中以PA，PB为边作?APBQ（保留作图痕迹，不写作法），并连接PQ交AB于点M．
【探究】（1）在点P运动过程中，对角线PQ的最小值为3，此时$\frac{AP}{AC}$的值为$\frac{1}{2}$；
【温馨提示】若你在探究此问题时出现困难，可参考如下分析思路：端点分别在两条平行线上的所有线段中，垂直于平行线的线段最短．
（2）如图2，若延长PA到点E，使AE=nPA（n为大于0的常数），以PE、PB为边作?PBQE，求对角线PQ的最小值和此时$\frac{AP}{AC}$的值；
【拓展】如图3，若P为AB边上的一动点，延长PA到点E，使AE=nPA（n为大于0的常数），以PE、PC为边作?PCQE．则对角线PQ的最小值为$\frac{12}{5}$，此时$\frac{AP}{AC}$的值为$\frac{4}{5（n+2）}$．

Answer 1

分析 操作：作平行四边形即可；
探究：（1）当PQ∥BC时，对角线PQ的最小值，且PQ=BC=3，即可得出$\frac{AP}{AC}$的值；
（2）由题可知：当QP⊥AC时，PQ最短．可以证到四边形PCBQ是矩形．从而可以得到PQ=BC=3，PC=QB=EP，由AE=nPA可以用AP表示AC，从而求出$\frac{AP}{AC}$的值．
（3）由题可知：当QP⊥AB时，PQ最短．过点C作CH⊥AB，垂足为H，可以证到四边形PHCQ是矩形，从而有QC=PH，PQ=HC．由AE=nPA可以用AP表示EH．易证△AHC∽△ACB从而可以求出AH=$\frac{16}{5}$，HC=$\frac{12}{5}$，从而有PQ=HC=$\frac{12}{5}$，EH=nPA+$\frac{16}{5}$，则有EH=2（n+1）AP=nPA+$\frac{16}{5}$，从而求出AP=$\frac{16}{5n+10}$，进而求出$\frac{AP}{AC}$的值．

解答 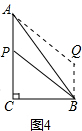解：操作：所作平行四边形如图4所示；
探究：（1）∵四边形APBQ是平行四边形，
∴AP∥BQ，
∴当PQ∥BC时，对角线PQ的最小值，且PQ=BC=3，
∵AC=4，
∴AP=BQ，AQ=BP，且BQ=PC，
∴AP=PC=2，
∴$\frac{AP}{AC}$=$\frac{1}{2}$；
故答案分别为：3、$\frac{1}{2}$．

（2）如图5，
由题可知：当QP⊥AC时，PQ最短．
∵QP⊥AC，∠ACB=90°，
∴∠APQ=∠C=90°．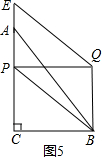
∴PQ∥BC．
∵四边形PBQE是平行四边形，
∴EP∥BQ，EP=BQ．
∵PC∥BQ，PQ∥BC，∠C=90°，
∴四边形PCBQ是矩形．
∴QB=PC，PQ=BC=3．
∴EP=PC．
∵AE=nPA，
∴PC=EP=EA+AP
=nPA+AP
=（n+1）AP．
∴AC=AP+PC
=AP+（n+1）AP
=（n+2）AP．
∴$\frac{AP}{AC}$=$\frac{AP}{（n+2）AP}$=$\frac{1}{n+2}$．

（3）过点C作CH⊥AB，垂足为H，如图6，
由题可知：当QP⊥AB时，PQ最短．
∵QP⊥AB，CH⊥AB，
∴∠APQ=∠AHC=90°．
∴PQ∥HC．
∵四边形PCQE是平行四边形，
∴EP∥CQ，EP=CQ．
∵PH∥CQ，PQ∥HC，∠PHC=90°，
∴四边形PHCQ是矩形．
∴QC=PH，PQ=HC．
∴EP=PH．
∵AE=nPA，
∴EP=EA+AP
=nPA+AP
=（n+1）AP．
∴EH=2EP=2（n+1）AP．
∵∠ACB=90°，BC=3，AC=4，
∴AB=5．
∵∠HAC=∠CAB，∠AHC=∠ACB=90°，
∴△AHC∽△ACB．
∴$\frac{AH}{AC}$=$\frac{HC}{CB}$=$\frac{AC}{AB}$．
∵BC=3，AC=4，AB=5，
∴$\frac{AH}{4}$=$\frac{HC}{3}$=$\frac{4}{5}$．
∴AH=$\frac{16}{5}$，HC=$\frac{12}{5}$．
∴PQ=HC=$\frac{12}{5}$，EH=AE+AH=nPA+$\frac{16}{5}$．
∴EH=2（n+1）AP=nPA+$\frac{16}{5}$．
∴（2n+2-n）AP=$\frac{16}{5}$．
∴AP=$\frac{16}{5n+10}$．
∴$\frac{AP}{AC}$=$\frac{16}{4（5n+10）}$=$\frac{4}{5n+10}$．
故答案分别为：$\frac{12}{5}$、$\frac{4}{5n+10}$．

点评 本题考查了相似三角形的综合题，以及平行线之间的距离、平行线的判定、相似三角形的判定与性质、矩形的判定与性质、平行四边形的性质、勾股定理等知识，具有一定的综合性；本题还考查了阅读能力，体现了自主探究与合作交流相结合的新课程理念，是一道好题．