Question

已知△ABC中，AB＝AC＝6，cosB＝，点O在边AB上，⊙O过点B且分别与边AB、BC，另有交点D、E，但⊙O与边AC不相交，又EF⊥AC，垂足为F．设OB＝x，CF＝y．

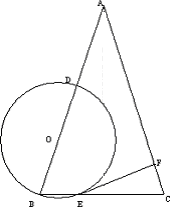
(1)求证：直线EF是⊙O的切线；

(2)求y关于x的函数解析式．

(3)当直线DF与⊙O相切时，求OB的长．

Answer 1

答案：
解析：

(1)连结OE，那么OE＝OB， 　　得∠OBE＝∠OEB． 　　∵AB＝AC，∴∠OBE＝∠C． 　　∴∠OEB＝∠C，得OE∥AC． 　　∵EF⊥AC，∴EF⊥OE． 　　∵点E在圆O上， 　　∴EF是圆O的切线． 　　(2)作AH⊥BC，H为垂足， 　　那么BH＝BC． 　　∵AB＝6，cosB＝， 　　∴BH＝2，BC＝4． 　　∵OE∥AC， 　　∴＝，即＝，得BE＝x， 　　∴EC＝4－x． 　　在直角三角形ECF中，cosC＝cosB＝ 　　∴CF＝EC·cosC＝(4－x)· 　　∴所求函数解析式y＝－x 　　自变量x的取值范围为0＜x≤． 　　(3)画出示意图． 　　解法一：连结OE、DE、OF． 　　由DF与圆O相切，∴FD＝FE． 　　又OD＝OE， 　　∴OF垂直(平分)DE． 　　由∠DEB＝90°， 　　∴BC⊥DE．∴OF∥BC． 　　这时，OB＝CF， 　　得－x＝x， 　　解得x＝，即OB＝．