练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图所示,五边形ABCDE是张大爷十年前承包的一块土地的示意图. 经过多年开垦荒地,现已变成如图所示的形状,但承包土地与开垦荒地的分界小路( 即图中折线CDE)还保留着,张大爷想过E点修一条直路,直路修好后,要保持直路左边的土地面积与承包时的一样多,右边的土地面积与开垦的荒地面积一样多.请你用有关的几何知识,按张大爷的要求设计出修路方案.(不计分界小路与直路的占地面积).

    　　(1)写出设计方案,并在图中画出相应的图形;

    (2)说明方案设计理由.
    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

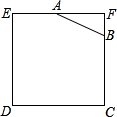    精英家教网如图所示，已知边长为4的正方形钢板有一个角锈蚀，其中AF=2，BF=1，为了合理利用这块钢板．将在五边形EABCD内截取一个矩形块MDNP，使点P在AB上，且要求面积最大，求钢板的最大利用率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

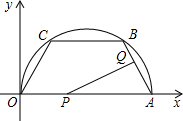    如图所示，平面直角坐标系中，四边形OABC内接于半圆，其中OA为直径，弦AB=OC=3cm，∠OAB=60°，精英家教网P点从O点出发，以2cm/s的速度向A运动；同时，Q从A点出发，沿边AB向B以1cm/s的速度运动．
    （1）求运动x秒后Q点的坐标（用含x的式子表示）．
    （2）是否存在x，使得PQ∥OB？若存在，则求出x的值；若不存在，说明理由．
    （3）求BC的长．
    （4）当P、Q运动时，写出五边形OPQBC的面积y与时间x之间的函数关系式，并写出x的取值范围（不包括点P在O、A两点时的情况）．求出五边形OPQBC的面积的最小值及此时x的值？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

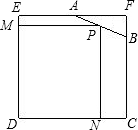    精英家教网如图所示，在边长为4的正方形EFCD上截去一角，成为五边形ABCDE，其中AF=2，BF=1，在AB上取一点P，设P到DE的距离PM=x，P到CD的距离PN=y，试写出矩形PMDN的面积S与x之间的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

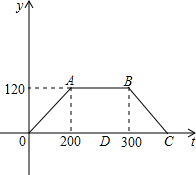    小明参加汽车驾驶培训，在实际操作考试时，被要求进行启动加速、匀速运行、制动减速三个连贯过程，在加速和减速运动过程中，路程和速度均满足关系s=v0t+
    12
    at2    ，v0为加速或减速的起始速度，加速时a为正，减速时a为负，匀速时a=0，加速或减速t秒后的瞬时速度v=v0+at，小明在操作中瞬时速度v与时间t的关系如图所示，其中OA为匀加速，AB为匀速，BC为匀减速．
    （1）若减速过程与加速过程完全相反，即BC与OA关于AB的中垂线成轴对称，求BC的解析式．
    （2）当0≤t≤300时，求汽车行驶的路程s与时间t的函数关系式．
    （3）汽车行驶t秒后，
    ①若经途中D点，过点D作垂线交AB于点E，试证明汽车行驶的路程恰等于四边形OAED的面积．
    ②若汽车行驶至M点，过点M做垂线交BC于点N，汽车行驶的路程是否等于五边形OABNM的面积呢？试说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图所示，五边形ABCDE中，AB=AE，BC=DE，∠ABC=∠AED，点F是CD的中点．
    求证：AF⊥CD．

    查看答案和解析>>

    同步练习册答案