
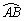 所对的圆心角为120°,已知圆的半径为2cm,并建立如图所示的直角坐标系。
所对的圆心角为120°,已知圆的半径为2cm,并建立如图所示的直角坐标系。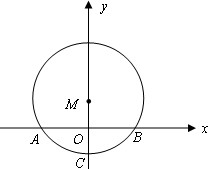
| 解:(1)如图,连接MA、MB, 则∠AMB=120°, ∴∠CMB=60°,∠OBM=30度 ∴OM= 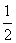 MB=1, MB=1,∴M(0,1)。 (2)由A,B,C三点的特殊性与对称性, 知经过A,B,C三点的抛物线的解析式为y=ax2+c ∵OC=MC-MO=1,  ∴C(0,-1),B( 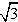 ,0) ,0)∴ 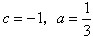 ∴ 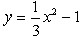 。 。(3)∵ 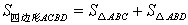 又 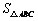 与AB均为定值 与AB均为定值∴当△ABD边AB上的高最大时,S△ABD最大, 此时点D为⊙M与y轴的交点,如图 ∴  。 。 |
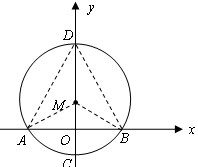 |
(4)如图,∵△ABC为等腰三角形,∠ABC=30°,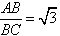 ∴△ABC∽△PAB等价于∠PAB=30°,  设 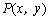 且x>0,则 且x>0,则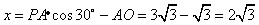 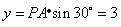 又∵ 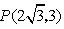 的坐标满足 的坐标满足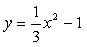 ∴在抛物线 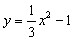 上,存在点 上,存在点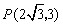 使 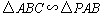 由抛物线的对称性,知点 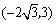 也符合题意 也符合题意∴存在点P,它的坐标为 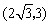 或 或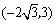 。 。 |
 |


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源:2009-2010学年九年级(下)数学综合测试卷(解析版) 题型:解答题
 所对的圆心角为120°,已知圆的半径为2cm,并建立如图所示的直角坐标系.
所对的圆心角为120°,已知圆的半径为2cm,并建立如图所示的直角坐标系.
查看答案和解析>>
科目:初中数学 来源:第27章《二次函数》中考题集(46):27.3 实践与探索(解析版) 题型:解答题
 所对的圆心角为120°,已知圆的半径为2cm,并建立如图所示的直角坐标系.
所对的圆心角为120°,已知圆的半径为2cm,并建立如图所示的直角坐标系.
查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(48):2.8 二次函数的应用(解析版) 题型:解答题
 所对的圆心角为120°,已知圆的半径为2cm,并建立如图所示的直角坐标系.
所对的圆心角为120°,已知圆的半径为2cm,并建立如图所示的直角坐标系.
查看答案和解析>>
科目:初中数学 来源:第20章《二次函数和反比例函数》中考题集(43):20.5 二次函数的一些应用(解析版) 题型:解答题
 所对的圆心角为120°,已知圆的半径为2cm,并建立如图所示的直角坐标系.
所对的圆心角为120°,已知圆的半径为2cm,并建立如图所示的直角坐标系.
查看答案和解析>>
科目:初中数学 来源:2006年甘肃省酒泉市中考数学试卷(课标卷)(解析版) 题型:解答题
 所对的圆心角为120°,已知圆的半径为2cm,并建立如图所示的直角坐标系.
所对的圆心角为120°,已知圆的半径为2cm,并建立如图所示的直角坐标系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com