
”¾ĢāÄæ”æijÉĢ³”ĻśŹŪA”¢BĮ½ÖÖŠĀŠĶŠ”¼Ņµē£¬AŠĶĆæĢؽų¼Ū40ŌŖ£¬ŹŪ¼Ū50ŌŖ£¬BŠĶĆæĢؽų¼Ū32ŌŖ£¬ŹŪ¼Ū40ŌŖ£¬4ŌĀ·ŻŹŪ³öAŠĶ40ĢØ£¬ĒŅĻśŹŪÕāĮ½ÖÖŠ”¼Ņµē¹²»ńĄū²»ÉŁÓŚ800ŌŖ£®
£Ø1£©Ēó4ŌĀ·ŻŹŪ³öBŠĶŠ”¼ŅµēÖĮÉŁ¶ąÉŁĢØ£æ
£Ø2£©¾ŹŠ³”µ÷²é£¬5ŌĀ·ŻAŠĶŹŪ¼ŪĆæ½µµĶ1ŌŖ£¬ĻśĮ潫Ōö¼Ó10ĢØ£»BŠĶŹŪ¼ŪĆæ½µµĶ1ŌŖ£¬ĻśĮ潫ŌŚ4ŌĀ·Ż×īµĶĻśĮæµÄ»ł“”ÉĻŌö¼Ó15ĢØ£®ĪŖ¾”æÉÄÜČĆĻū·ŃÕß»ńµĆŹµ»Ż£¬ÉĢ³”¼Ę»®5ŌĀ·ŻA”¢BĮ½ÖÖŠ”¼Ņµē¶¼½µµĶĻąĶ¬¼Ūøń£¬ĒŅĻ£ĶūĻśŹŪÕāĮ½ÖÖŠ”¼Ņµē¹²»ńĄū965ŌŖ£¬ŌņÕāĮ½ÖÖŠ”¼Ņµē¶¼Ó¦½µµĶ¶ąÉŁŌŖ£æ
”¾“š°ø”æ£Ø1£©4ŌĀ·ŻŹŪ³öBŠĶŠ”¼ŅµēÖĮÉŁ50ĢØ£»£Ø2£©Į½ÖÖŠĶŗŵĊ”¼Ņµē¶¼½µ¼Ū3ŌŖ£®
”¾½āĪö”æ
£Ø1£©Éč4ŌĀ·ŻŹŪ³öBŠĶŠ”¼ŅµēxĢØ£¬øł¾Ż”°ĻśŹŪÕāĮ½ÖÖŠ”¼Ņµē¹²»ńĄū²»ÉŁÓŚ800ŌŖ”±ĮŠ³ö²»µČŹ½²¢½ā“š£»
£Ø2£©ÉčĮ½ÖÖŠĶŗŵĊ”¼Ņµē¶¼½µ¼ŪyŌŖ£¬øł¾Ż”°ĻśŹŪĄūČó£½£ØŹŪ¼Ū©½ų¼Ū£©”ĮĻśŹŪŹżĮæ”±ĮŠ³ö·½³Ģ²¢½ā“š£®
½ā£ŗ£Ø1£©Éč4ŌĀ·ŻŹŪ³öBŠĶŠ”¼ŅµēxĢØ£¬
øł¾ŻĢāŅā£¬µĆ£Ø50©40£©”Į40+£Ø40©32£©x”Ż800£®
½āµĆx”Ż50£®
“š£ŗ4ŌĀ·ŻŹŪ³öBŠĶŠ”¼ŅµēÖĮÉŁ50ĢØ£»
£Ø2£©ÉčĮ½ÖÖŠĶŗŵĊ”¼Ņµē¶¼½µ¼ŪyŌŖ£¬øł¾ŻĢāŅā£¬µĆ£ŗ
![]()
ÕūĄķ£¬µĆ![]() £®
£®
½āµĆy1£½3£¬y2£½2.2£®
ĪŖĮĖČĆĻū·ŃÕߵƵ½øü¶ąµÄŹµ»Ż£¬ĖłŅŌy£½3·ūŗĻĢāŅā£®
“š£ŗĮ½ÖÖŠĶŗŵĊ”¼Ņµē¶¼½µ¼Ū3ŌŖ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
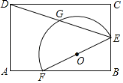
”¾ĢāÄæ”æČēĶ¼£¬¾ŲŠĪABCDÖŠ£¬AB£½3£¬BC£½2£¬EĪŖBCµÄÖŠµć£¬AF£½1£¬ŅŌEFĪŖÖ±¾¶µÄ°ėŌ²ÓėDE½»ÓŚµćG£¬ŌņĮÓ»”![]() µÄ³¤ĪŖ_____£®
µÄ³¤ĪŖ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ę½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŅŌ![]() ĪŖŌ²ŠÄ£¬ŌŚµŚŅ»ĻóĻŽÄŚ»Ō²»”£¬ÓėĖ«ĒśĻß½»ÓŚĮ½µć£¬µć
ĪŖŌ²ŠÄ£¬ŌŚµŚŅ»ĻóĻŽÄŚ»Ō²»”£¬ÓėĖ«ĒśĻß½»ÓŚĮ½µć£¬µć![]() ŹĒŌ²»”ÉĻŅ»øö¶Æµć£¬Į¬½į
ŹĒŌ²»”ÉĻŅ»øö¶Æµć£¬Į¬½į![]() ²¢ŃÓ³¤½»µŚČżĻóĻŽµÄĖ«ĒśĻßÓŚµć
²¢ŃÓ³¤½»µŚČżĻóĻŽµÄĖ«ĒśĻßÓŚµć![]() £¬×÷
£¬×÷![]() Öį£¬
Öį£¬![]() Öį£¬Ö»ÓŠµ±
Öį£¬Ö»ÓŠµ±![]() Ź±£¬
Ź±£¬![]() £¬Ōņ
£¬Ōņ![]() µÄ°ė¾¶ĪŖ_____________________£®
µÄ°ė¾¶ĪŖ_____________________£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
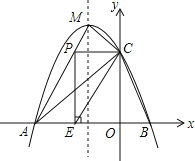
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻß![]() ÓėxÖį½»ÓŚA”¢BĮ½µć£¬ÓėyÖį½»ÓŚµć
ÓėxÖį½»ÓŚA”¢BĮ½µć£¬ÓėyÖį½»ÓŚµć![]() £¬ĒŅ“ĖÅ×ĪļĻߵĶ„µć×ų±źĪŖ
£¬ĒŅ“ĖÅ×ĪļĻߵĶ„µć×ų±źĪŖ![]() £®
£®
![]() Ēó“ĖÅ×ĪļĻߵĽāĪöŹ½£»
Ēó“ĖÅ×ĪļĻߵĽāĪöŹ½£»
![]() ÉčµćDĪŖŅŃÖŖÅ×ĪļĻ߶Ō³ĘÖįÉĻµÄČĪŅāŅ»µć£¬µ±
ÉčµćDĪŖŅŃÖŖÅ×ĪļĻ߶Ō³ĘÖįÉĻµÄČĪŅāŅ»µć£¬µ±![]() Óė
Óė![]() Ć껿ĻąµČŹ±£¬ĒóµćDµÄ×ų±ź£»
Ć껿ĻąµČŹ±£¬ĒóµćDµÄ×ų±ź£»
![]() µćPŌŚĻ߶ĪAMÉĻ£¬µ±PCÓėyÖį“¹Ö±Ź±£¬¹żµćP×÷xÖįµÄ“¹Ļߣ¬“¹×ćĪŖE£¬½«
µćPŌŚĻ߶ĪAMÉĻ£¬µ±PCÓėyÖį“¹Ö±Ź±£¬¹żµćP×÷xÖįµÄ“¹Ļߣ¬“¹×ćĪŖE£¬½«![]() ŃŲÖ±ĻßCE·ÕŪ£¬Ź¹µćPµÄ¶ŌÓ¦µć
ŃŲÖ±ĻßCE·ÕŪ£¬Ź¹µćPµÄ¶ŌÓ¦µć![]() ÓėP”¢E”¢C“¦ŌŚĶ¬Ņ»Ę½ĆęÄŚ£¬ĒėĒó³öµć
ÓėP”¢E”¢C“¦ŌŚĶ¬Ņ»Ę½ĆęÄŚ£¬ĒėĒó³öµć![]() ×ų±ź£¬²¢ÅŠ¶Ļµć
×ų±ź£¬²¢ÅŠ¶Ļµć![]() ŹĒ·ńŌŚøĆÅ×ĪļĻßÉĻ£®
ŹĒ·ńŌŚøĆÅ×ĪļĻßÉĻ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
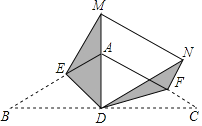
”¾ĢāÄæ”æČēĶ¼£¬ŌŚµČŃü”÷ABCÖŠ£¬AB£½AC£½2£¬”ĻABC£½30”ć£¬ADĪŖBC±ßÉĻµÄøߣ¬E”¢F·Ö±šĪŖAB”¢AC±ßÉĻµÄµć£¬½«”÷ABC·Ö±šŃŲDE”¢DFÕŪµž£¬Ź¹µćBĀäŌŚDAµÄŃÓ³¤ĻßÉĻµćM“¦£¬µćCĀäŌŚµćN“¦£¬Į¬½ÓMN£¬ČōMN”ĪAC£¬ŌņAFµÄ³¤ŹĒ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ę½ĆęÖ±½Ē×ų±źĻµ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() £¬µć
£¬µć![]() ŌŚ
ŌŚ![]() ÖįµÄÕż°ėÖįÉĻ£¬µć
ÖįµÄÕż°ėÖįÉĻ£¬µć![]() ŹĒ
ŹĒ![]() ÖįÕż°ėÖįÉĻŅ»¶Æµć£¬Į¬½Ó
ÖįÕż°ėÖįÉĻŅ»¶Æµć£¬Į¬½Ó![]() £¬ŅŌ
£¬ŅŌ![]() ĪŖ±ß³¤£¬ŌŚ
ĪŖ±ß³¤£¬ŌŚ![]() µÄÓŅ²ą×÷µČ±ß
µÄÓŅ²ą×÷µČ±ß![]() £®Éčµć
£®Éčµć![]() µÄŗį×ų±źĪŖ
µÄŗį×ų±źĪŖ![]() £¬µć
£¬µć![]() µÄׯ×ų±źĪŖ
µÄׯ×ų±źĪŖ![]() £¬Ōņ
£¬Ōņ![]() Óė
Óė![]() µÄŗÆŹż¹ŲĻµŹ½ŹĒ________£®
µÄŗÆŹż¹ŲĻµŹ½ŹĒ________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
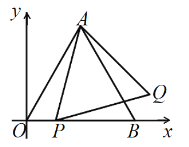
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻß![]()
![]() ½»
½»![]() ÖįÓŚµć
ÖįÓŚµć![]() £¬
£¬![]() £¬½»
£¬½»![]() ÖįÓŚµć
ÖįÓŚµć![]() £¬ĒŅÅ×ĪļĻߵĶŌ³ĘÖį¾¹żµć
£¬ĒŅÅ×ĪļĻߵĶŌ³ĘÖį¾¹żµć![]() £¬¹żµć
£¬¹żµć![]() µÄÖ±Ļß
µÄÖ±Ļß![]() ½»Å×ĪļĻßÓŚĮķŅ»µć
½»Å×ĪļĻßÓŚĮķŅ»µć![]() £¬µć
£¬µć![]() ŹĒøĆÅ×ĪļĻßÉĻŅ»µć£¬Į¬½Ó
ŹĒøĆÅ×ĪļĻßÉĻŅ»µć£¬Į¬½Ó![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £®
£®

£Ø1£©ĒóÖ±Ļß![]() ¼°Å×ĪļĻßµÄŗÆŹż±ķ“ļŹ½£»
¼°Å×ĪļĻßµÄŗÆŹż±ķ“ļŹ½£»
£Ø2£©ŹŌĪŹ£ŗ![]() ÖįÉĻŹĒ·ń“ęŌŚÄ³Ņ»µć
ÖįÉĻŹĒ·ń“ęŌŚÄ³Ņ»µć![]() £¬Ź¹µĆŅŌµć
£¬Ź¹µĆŅŌµć![]() £¬
£¬![]() £¬
£¬![]() ĪŖ¶„µćµÄ
ĪŖ¶„µćµÄ![]() Óė
Óė![]() ĻąĖĘ£æČōĻąĖĘ£¬ĒėĒó³ö“ĖŹ±µć
ĻąĖĘ£æČōĻąĖĘ£¬ĒėĒó³ö“ĖŹ±µć![]() µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
£Ø3£©Čōµć![]() ŹĒÖ±Ļß
ŹĒÖ±Ļß![]() ÉĻ·½µÄÅ×ĪļĻßÉĻŅ»¶Æµć£Ø²»Óėµć
ÉĻ·½µÄÅ×ĪļĻßÉĻŅ»¶Æµć£Ø²»Óėµć![]() £¬
£¬![]() ÖŲŗĻ£©£¬¹ż
ÖŲŗĻ£©£¬¹ż![]() ×÷
×÷![]() ½»Ö±Ļß
½»Ö±Ļß![]() ÓŚµć
ÓŚµć![]() £¬ŅŌ
£¬ŅŌ![]() ĪŖÖ±¾¶×÷
ĪŖÖ±¾¶×÷![]() £¬Ōņ
£¬Ōņ![]() ŌŚÖ±Ļß
ŌŚÖ±Ļß![]() ÉĻĖł½ŲµĆµÄĻ߶Ī³¤¶ČµÄ×ī“óÖµµČÓŚ_______£®£ØÖ±½ÓŠ“³ö“š°ø£©
ÉĻĖł½ŲµĆµÄĻ߶Ī³¤¶ČµÄ×ī“óÖµµČÓŚ_______£®£ØÖ±½ÓŠ“³ö“š°ø£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗ![]() ŹĒ
ŹĒ![]() µÄÖ±¾¶£¬
µÄÖ±¾¶£¬![]() µÄŃÓ³¤ĻßÉĻÓŠŅ»µć
µÄŃÓ³¤ĻßÉĻÓŠŅ»µć![]() £¬
£¬![]() ŹĒ
ŹĒ![]() µÄĒŠĻߣ¬ĒŠµćĪŖ
µÄĒŠĻߣ¬ĒŠµćĪŖ![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() £¬“¹×ćĪŖ
£¬“¹×ćĪŖ![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £®
£®
£Ø1£©ČēĶ¼1£¬ĒóÖ¤£ŗ![]() £»
£»
£Ø2£©ČēĶ¼2£¬![]() ŹĒ
ŹĒ![]() ÉĻµÄµć£¬Į¬½Ó
ÉĻµÄµć£¬Į¬½Ó![]() ”¢
”¢![]() £¬Čō
£¬Čō![]() £¬
£¬
ĒóÖ¤£ŗ![]() £»
£»
£Ø3£©ČēĶ¼3£¬ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬µć![]() ŌŚ
ŌŚ![]() ÉĻ£¬µć
ÉĻ£¬µć![]() ŌŚ
ŌŚ![]() ÉĻ£¬Į¬½Ó
ÉĻ£¬Į¬½Ó![]() ŗĶ
ŗĶ![]() Ļą½»ÓŚµć
Ļą½»ÓŚµć![]() £¬ŃÓ³¤
£¬ŃÓ³¤![]() µ½µć
µ½µć![]() £¬Į¬½Ó
£¬Į¬½Ó![]() ”¢
”¢![]() £¬Čō
£¬Čō![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬ĒóĻ߶Ī
£¬ĒóĻ߶Ī![]() µÄ³¤£®
µÄ³¤£®


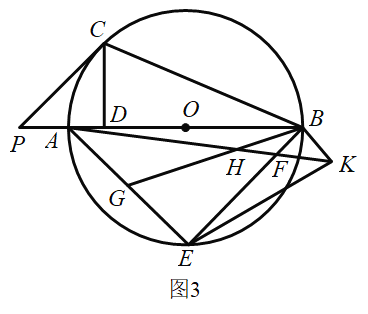
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ![]() ŹĒ”ŃOµÄÖ±¾¶£¬
ŹĒ”ŃOµÄÖ±¾¶£¬![]() £¬µć
£¬µć![]() ŌŚ”ŃOµÄ°ė¾¶
ŌŚ”ŃOµÄ°ė¾¶![]() ÉĻŌĖ¶Æ£¬
ÉĻŌĖ¶Æ£¬![]() £¬“¹×ćĪŖ
£¬“¹×ćĪŖ![]() £¬
£¬![]() £¬
£¬![]() ĪŖ”ŃOµÄĒŠĻߣ¬ĒŠµćĪŖ
ĪŖ”ŃOµÄĒŠĻߣ¬ĒŠµćĪŖ![]() £®
£®
£Ø1£©ČēĶ¼1£¬µ±![]() µćŌĖ¶Æµ½
µćŌĖ¶Æµ½![]() µćŹ±£¬Ēó
µćŹ±£¬Ēó![]() µÄ³¤£»
µÄ³¤£»
£Ø2£©ČēĶ¼2£¬µ±![]() µćŌĖ¶Æµ½
µćŌĖ¶Æµ½![]() µćŹ±£¬Į¬½Ó
µćŹ±£¬Į¬½Ó![]() ”¢
”¢![]() £¬ĒóÖ¤£ŗ
£¬ĒóÖ¤£ŗ![]() ”Ī
”Ī![]() £»
£»
£Ø3£©ČēĶ¼3£¬Éč![]() £¬
£¬![]() £¬ĒóyÓėxµÄ½āĪöŹ½²¢Ēó³öyµÄ×īŠ”Öµ£®
£¬ĒóyÓėxµÄ½āĪöŹ½²¢Ēó³öyµÄ×īŠ”Öµ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com