
【题目】如图,在矩形ABCD中,点O是AC的中点,AC=2AB,延长AB至G,使BG=AB,连接GO交BC于E,延长GO交AD于F,连接AE.
求证:(1)△ABC≌△AOG;
(2)猜测四边形AECF的形状并证明你的猜想.

【答案】(1)证明见解析;(2)四边形AECF是菱形;理由见解析
【解析】
(1)由已知条件得出AB=AO,AC=AG,由SAS证明△ABC≌△AOG即可;
(2)由矩形的性质得出∠ABC=90°,AD∥BC,得出∠OAF=∠OCE,由ASA证明△AOF≌△COE,得出OF=OE,得出四边形AECF是平行四边形,再由全等三角形的对应角相等得出∠AOG=∠ABC=90°,即可得出结论.
(1)证明:∵点O是AC的中点,
∴AO=CO=![]() AC,
AC,
∵AC=2AB,BG=AB,
∴AB=AO,AC=AG,
在△ABC和△AOG中, ,
,
∴△ABC≌△AOG(SAS);
(2)四边形AECF是菱形;理由如下:
∵四边形ABCD是矩形,
∴∠ABC=90°,AD∥BC,
∴∠OAF=∠OCE,
在△AOF和△COE中, ,
,
∴△AOF≌△COE(ASA),
∴OF=OE,
∴四边形AECF是平行四边形,
∵△ABC≌△AOG,
∴∠AOG=∠ABC=90°,
∴AC⊥EF,
∴四边形AECF是菱形.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
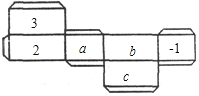
【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
(1)填空:a=______,b=______,c=______.
(2)先化简,再求值:-a2b+2(3ab2-a2b)-3(2ab2-a2b)+abc
查看答案和解析>>
科目:初中数学 来源: 题型:
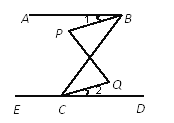
【题目】如图,已知∠ABC=63°,∠ECB=117°.
(1) AB与ED平行吗?为什么?
(2)若∠P=∠Q,则∠1与∠2是否相等?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组
请结合题意,完成本题解答过程.
(1)解不等式①,得 ,依据是 .
(2)解不等式②,得 .
(3)解不等式③,得 .
(4)把不等式①,②和③的解集在数轴上表示出来.
(5)从图中可以找出三个不等式解集的公共部分,得不等式组的解集 .
(6)根据不等式组的解集确立出该不等式组的最大整数解为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境
在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.
操作发现
(1)如图(1),小明把三角尺的60°角的顶点G放在CD上,若∠2=2∠1,求∠1的度数;
(2)如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明∠AEF与∠FGC之间的数量关系;
结论应用
(3)如图(3),小亮把三角尺的直角顶点F放在CD上,30°角的顶点E落在AB上.若∠AEG=α,则∠CFG等于______(用含α的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+4与反比例函数y= ![]() 的图象相交于A(﹣3,a)和B两点
的图象相交于A(﹣3,a)和B两点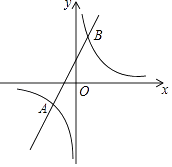
(1)求k的值;
(2)直线y=m(m>0)与直线AB相交于点M,与反比例函数的图象相交于点N.若MN=4,求m的值;
(3)直接写出不等式 ![]() >x的解集.
>x的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于不等式组 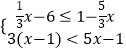 ,下列说法正确的是( )
,下列说法正确的是( )
A.此不等式组的正整数解为1,2,3
B.此不等式组的解集为﹣1<x≤ ![]()
C.此不等式组有5个整数解
D.此不等式组无解
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄冈农科院培育的“黄金8号”玉米种子的价格为5元/kg,如果一次购买2kg以上的种子,超过2kg部分的种子的价格打8折.
(Ⅰ)根据题意,填写下表:
购买种子的数量/kg 1.5 2 3.5 4 …
付款金额/元 7.5 16 …
(Ⅱ)设购买种子数量为xkg,付款金额为y元,求y关于x的函数解析式;
(Ⅲ)若小明帮奶奶一次购买该种子花费了30元,求他购买种子的数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程kx2+(2k+1)x+2=0.
(1)求证:无论k取任何实数时,方程总有实数根;
(2)当抛物线y=kx2+(2k+1)x+2图象与x轴两个交点的横坐标均为整数,且k为正整数时,若P(a,y1),Q(1,y2)是此抛物线上的两点,且y1>y2 , 请结合函数图象确定实数a的取值范围;
(3)已知抛物线y=kx2+(2k+1)x+2恒过定点,求出定点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com