
【题目】(1)解不等式2(4x-1)≥5x-8,并把它的解集在数轴上表示出来.
![]()
(2)如图,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别是A(-3,0),B(-6,-2)C(-2,-5).将△ABC向上平移3个单位长度,再向右平移5个单位长度,得到△A1B1C1.
①在平面直角坐标系xOy中画出△A1B1C1.
②求△A1B1C1的面积.

 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】2020年新型冠状病毒肺炎疫情肆虐,红星社区为了提高社区居民的身体素质,鼓励居民在家锻炼,特采购了一批跳绳免费发放,已知2根幸福牌跳绳和1根平安牌跳绳共需31元,2根平安牌跳绳和3根幸福牌跳绳共需54元.
(1)求幸福牌跳绳和平安牌跳绳的单价;
(2)已知该社区需要采购两种品牌的跳绳共60根,且平安牌跳绳的数量不少于幸福牌跳绳数量的2倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对![]() ,
,![]() 定义一种新运算
定义一种新运算![]() ,规定:
,规定:![]() (其中
(其中![]() ,
,![]() 均为非零常数),这里等式右边是通常的四则运算,例如:
均为非零常数),这里等式右边是通常的四则运算,例如:![]() ,已知
,已知![]() ,
,![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)若关于![]() 的不等式组
的不等式组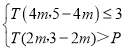 恰好有2个整数解,求实数
恰好有2个整数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类),并将调查的结果绘制成如下的两幅不完整的统计图,请根图中提供的信息,解答下列问题:
(1)参加调查的人数共有 人;
(2)将条形图补充完整;
(3)求在扇形图中表示“其它球类”的扇形的圆心角的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网店店主小李进了一批某种商品,每件进价10元.预售一段时间后发现:每天销售量![]() (件)与售价
(件)与售价![]() (元/件)之间成一次函数关系:
(元/件)之间成一次函数关系:![]() .
.
(1)小李想每天赚取利润150元,又要使所进的货尽快脱手,则售价定为多少合适?
(2)小李想每天赚取利润300元,这个想法能实现吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则Bn的坐标是( )

A.(2n﹣1,2n﹣1)B.(2n﹣1+1,2n﹣1)
C.(2n﹣1,2n﹣1)D.(2n﹣1,n)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备购进![]() 两种商品,
两种商品,![]() 种商品毎件的进价比
种商品毎件的进价比![]() 种商品每件的进价多20元,用3000元购进
种商品每件的进价多20元,用3000元购进![]() 种商品和用1800元购进
种商品和用1800元购进![]() 种商品的数量相同.商店将
种商品的数量相同.商店将![]() 种商品每件的售价定为80元,
种商品每件的售价定为80元,![]() 种商品每件的售价定为45元.
种商品每件的售价定为45元.
(1)![]() 种商品每件的进价和
种商品每件的进价和![]() 种商品每件的进价各是多少元?
种商品每件的进价各是多少元?
(2)商店计划用不超过1560元的资金购进![]() 两种商品共40件,其中
两种商品共40件,其中![]() 种商品的数量不低于
种商品的数量不低于![]() 种商品数量的一半,该商店有几种进货方案?
种商品数量的一半,该商店有几种进货方案?
(3)端午节期间,商店开展优惠促销活动,决定对每件![]() 种商品售价优惠
种商品售价优惠![]() (
(![]() )元,
)元,![]() 种商品售价不变,在(2)条件下,请设计出销售这40件商品获得总利润最大的进货方案.
种商品售价不变,在(2)条件下,请设计出销售这40件商品获得总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车销售公司经销某品牌A款汽车,随着汽车的普及,其价格也在不断下降,今年5月份A款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的A款汽车,去年销售额为90万元,今年销售额只有80万元.
(1)今年5月份A款汽车每辆售价多少万元?
(2)为了增加收入,汽车销售公司决定再经销同品牌的B款汽车,已知B款汽车每辆进价为7.5万元,每辆售价为10.5万元,A款汽车每辆进价为6万元,若卖出这两款汽车15辆后获利不低于38万元,问B款汽车至少卖出多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与x轴交于A,B两点(点A在点B的左侧)与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D,点E为y轴上一动点,CE的垂直平分线交抛物线于P,Q两点(点P在第三象限)

(1)求抛物线的函数表达式和直线BC的函数表达式;
(2)当△CDE是直角三角形,且∠CDE=90° 时,求出点P的坐标;
(3)当△PBC的面积为![]() 时,求点E的坐标.
时,求点E的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com