
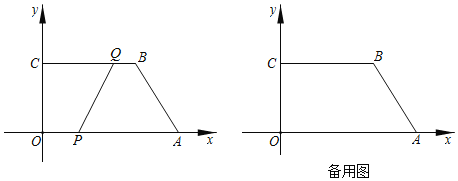
【题目】如图,在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(12,0),B(8,6),C(0,6).动点P从点O出发,以每秒3个单位长度的速度沿边向OA终点A运动;动点Q从点B同时出发,以每秒2个单位长度的速度沿边BC向终点C运动.设运动的时间为t秒,PQ![]() =y.
=y.
(1)直接写出y关于t的函数解析式及t的取值范围: ;
(2)当PQ=3![]() 时,求t的值;
时,求t的值;
(3)连接OB交PQ于点D,若双曲线![]() 经过点D,问k的值是否变化?若不变化,请求出k的值;若变化,请说明理由.
经过点D,问k的值是否变化?若不变化,请求出k的值;若变化,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)过点![]() 作
作![]() 于点
于点![]() ,由点
,由点![]() ,
,![]() 的出发点、速度及方向可找出当运动时间为
的出发点、速度及方向可找出当运动时间为![]() 秒时点
秒时点![]() ,
,![]() 的坐标,进而可得出
的坐标,进而可得出![]() ,
,![]() 的长,再利用勾股定理即可求出
的长,再利用勾股定理即可求出![]() 关于
关于![]() 的函数解析式(由时间
的函数解析式(由时间![]() 路程
路程![]() 速度可得出
速度可得出![]() 的取值范围);
的取值范围);
(2)将![]() 代入(1)的结论中可得出关于
代入(1)的结论中可得出关于![]() 的一元二次方程,解之即可得出结论;
的一元二次方程,解之即可得出结论;
(3)连接![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,利用勾股定理可求出
,利用勾股定理可求出![]() 的长,由
的长,由![]() 可得出
可得出![]() ,利用相似三角形的性质结合可
,利用相似三角形的性质结合可![]() 求出
求出![]() ,由
,由![]() 可得出
可得出![]() ,在
,在![]() 中可求出
中可求出![]() 及
及![]() 的值,由
的值,由![]() ,
,![]() 可求出点
可求出点![]() 的坐标,再利用反比例函数图象上点的坐标特征即可求出
的坐标,再利用反比例函数图象上点的坐标特征即可求出![]() 值,此题得解.
值,此题得解.
解:(1)过点![]() 作
作![]() 于点
于点![]() ,如图1所示.
,如图1所示.
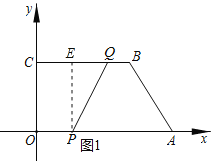
当运动时间为![]() 秒时时
秒时时![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
![]() ,|
,|![]() ,
,
![]() ,
,
![]() .
.
故答案为:![]() .
.
(2)当![]() 时,
时,![]() ,
,
整理,得:![]() ,
,
解得:![]() .
.
(3)经过点![]() 的双曲线
的双曲线![]() 的
的![]() 值不变.
值不变.
连接![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,如图2所示.
,如图2所示.

![]() ,
,![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
![]() 经过点
经过点![]() 的双曲线
的双曲线![]() 的
的![]() 值为
值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为6,E,F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.

(1)求证:EF=MF;
(2)若AE=2,求FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只箱子沿着斜面向上运动,箱高AB=1.3cm,当BC=2.6m时,点B离地面的距离BE=1m,则此时点A离地面的距离是( )
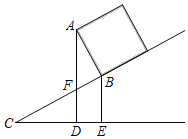
A.2.2mB.2mC.1.8mD.1.6m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABD内接于⊙O,AB为⊙O的直径,C为弧AD的中点,CH⊥AB于点E,交AD于点P,交⊙O于点H,连接DH,连接BC交AD于点F.下列结论中:①DH⊥CB;②CP=PF;③CH=AD;④APAD=CFCB;⑤若⊙O的半径为5,AF=![]() ,则CH=
,则CH=![]() .正确的有( )
.正确的有( )

A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
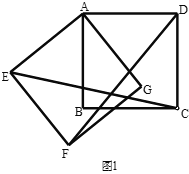
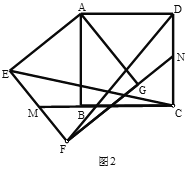
【题目】已知:正方形![]() 绕点
绕点![]() 顺时针旋转至正方形
顺时针旋转至正方形![]() ,连接
,连接![]() .
.
(1)如图,求证:![]() ;
;
(2)如图,延长![]() 交
交![]() 于
于![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,在不添加任何辅助线的情况下,请直接写出如图中的四个角,使写出的每一个角的大小都等于旋转角.
,在不添加任何辅助线的情况下,请直接写出如图中的四个角,使写出的每一个角的大小都等于旋转角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人定制了一批地砖,每块地砖(如图(1)所示)是边长为0.5米的正方形![]() .点E、F分别在边
.点E、F分别在边![]() 和
和![]() 上,
上,![]() 、
、![]() 和四边形
和四边形![]() 均由单一材料制成,制成
均由单一材料制成,制成![]() 、
、![]() 和四边形
和四边形![]() 的三种材料的价格依次为每平方米30元、20元、10元.若将此种地砖按图(2)所示的形式铺设,且中间的阴影部分组成正方形
的三种材料的价格依次为每平方米30元、20元、10元.若将此种地砖按图(2)所示的形式铺设,且中间的阴影部分组成正方形![]() .设
.设![]() .
.


(1)![]() ________,
________,![]() _________.(用含有x的代数式表示).
_________.(用含有x的代数式表示).
(2)已知烧制该种地砖平均每块需加工费0.35元,若要![]() 长大于0.1米,且每块地砖的成本价为4元(成本价=材料费用+加工费用),则
长大于0.1米,且每块地砖的成本价为4元(成本价=材料费用+加工费用),则![]() 长应为多少米?
长应为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
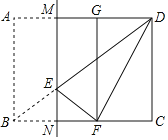
【题目】如图,在矩形ABCD中,AB:BC=3:4,点E是对角线BD上一动点(不与点B,D重合),将矩形沿过点E的直线MN折叠,使得点A,B的对应点G,F分别在直线AD与BC上,当△DEF为直角三角形时,CN:BN的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.
(1)求证:四边形ADEF是平行四边形;
(2)若∠ABC=60°,BD=6,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
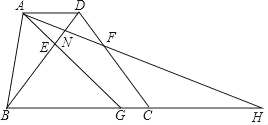
【题目】如图,在梯形ABCD中,AD∥BC,BC=18,DB=DC=15,点E、F分别在线段BD、CD上,DE=DF=5.AE的延长线交边BC于点G,AF交BD于点N、其延长线交BC的延长线于点H.
(1)求证:BG=CH;
(2)设AD=x,△ADN的面积为y,求y关于x的函数解析式,并写出它的定义域;
(3)联结FG,当△HFG与△ADN相似时,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com