Question

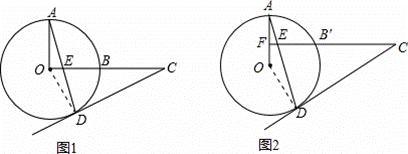
已知OA、OB是⊙O的两条半径，且OA⊥BC，C为OB延长线上任意一点，过点C作CD切⊙O于点D，连接AD，交OC过于点E。

（1）求证：CD=CE;

(2)若将图1中的半径OB所在的直线向上平行移动，交⊙O于,其他条件不变，如图2，那么上述结论CD=CE还成立吗？为什么？

图1

	图2

 

Answer 1

解：（1）△CDE是等腰三角形．理由如下：
连接OD，则OD⊥CD，∠CDE+∠ODA=90°；
在Rt△AOE中，∠AEO+∠A=90°，
在⊙O中，∵OA=OD，
∴∠A=∠ODA，∠CDE=∠AEO，
又∵∠AEO=∠CED，
∴∠CED=∠CDE，
∴CD=CE，
即△CDE是等腰三角形；

（2）结论仍然成立．理由如下：
∵将原来的半径OB所在直线向上平行移动，
∴CF⊥AO于F，
在Rt△AFE中，∠A+∠AEF=90°，
连接OD，则∠ODA+∠CDE=90°，且OA=OD，
故可得∠A=∠ODA，∠AEF=∠CDE，
又∵∠AEF=∠CED，
∴∠CED=∠CDE，
∴CD=CE．
故△CDE是等腰三角形．