
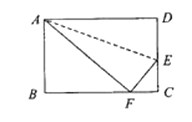
【题目】如图,一张长方形纸片宽AB=DC=8 cm,长BC=AD=10 cm,∠B=∠C=∠D=∠BAD=90°.现将纸片折叠,使顶点D落在BC边上的点F处(折痕为AE),求EC的长.
科目:初中数学 来源: 题型:
【题目】已知一次函数y=ax+b的图象经过点A(1,3)且与y=2x-3 平行.
(1)求出a,b.写出y 与x 的函数关系;
(2)求当x=-2 时,y的值,当y=10 时,x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
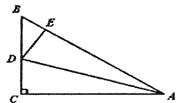
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB于点E,则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④若AC=4BE,则S△ABC=8S△BDE其中正确的有( )
A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
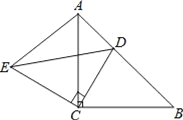
【题目】已知,如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)求证:2CD2=AD2+DB2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一段长为250km的高速公路需要维修,现由甲、乙两个工程队先后接力完成,共用时15天,已知甲工程队每天维修20km,乙工程队每天维修15km.求甲、乙两个工程队分别维修了多长的高速公路?(用一元一次方程解决问题)
查看答案和解析>>
科目:初中数学 来源: 题型:
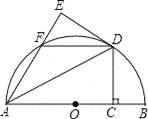
【题目】如图,AB是半圆O的直径,点C为半径OB上一点,过点C作CD丄AB交半圆O于点D,将△ACD沿AD折叠得到△AED,AE交半圆于点F,连接DF.
(1)求证:DE是半圆的切线:
(2)连接0D,当OC=BC时,判断四边形ODFA的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,I是ABC的内心,AI向延长线和△ABC的外接圆相交于点D,连接BI,BD,DC下列说法中错误的一项是( )
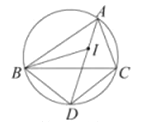
A.线段DB绕点D顺时针旋转一定能与线段DC重合
B.线段DB绕点D顺时针旋转一定能与线段DI熏合
C.∠CAD绕点A顺时针旋转一定能与∠DAB重合
D.线段ID绕点I顺时针旋转一定能与线段IB重合
查看答案和解析>>
科目:初中数学 来源: 题型:
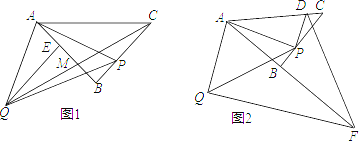
【题目】如图1,![]() 为等腰三角形,
为等腰三角形,![]() ,点
,点![]() 在线段
在线段![]() 上(不与
上(不与![]() 重合),以
重合),以![]() 为腰长作等腰直角
为腰长作等腰直角![]() ,
,![]() 于
于![]() .
.
(1)求证:![]() ;
;
(2)连接![]() 交
交![]() 于
于![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
(3)如图2,过![]() 作
作![]() 于
于![]() 的延长线于点
的延长线于点![]() ,过
,过![]() 点作
点作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时(不与
上运动时(不与![]() 重合),式子
重合),式子![]() 的值会变化吗?若不变,求出该值;若变化,请说明理由..
的值会变化吗?若不变,求出该值;若变化,请说明理由..
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小红两名同学在学习“概率”时,做掷骰子(质地均匀的正方体)试验.
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 7 | 9 | 6 | 8 | 20 | 10 |
(1)她们在一次试验中共掷骰子60次,试验的结果如下:
①填空:此次试验中“5点朝上”的频率为________;
②小红说:“根据试验,出现5点的概率最大.”她的说法正确吗?为什么?
(2)小颖和小红在试验中如果各掷一枚骰子,那么两枚骰子朝上的点数之和为多少时的概率最大?试用列表法或画树状图法加以说明,并求出其概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com