
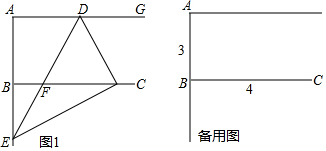
分析 (1)首先证明,∠CBE=90°,∠BCE=30°,根据tan30°=$\frac{BE}{BC}$,即可解决问题.
(2)如图2中,作DM⊥BC于M.只要证明△DCM∽△CEB,得$\frac{DM}{CB}$=$\frac{CM}{EB}$,由此即可解决问题.
(3)先证明∠EDA=∠EDC,由EA⊥DA,EC⊥DC,推出EA=EC=x+3,在Rt△BCE中,根据EC2=BE2+BC2,列出方程即可解决问题.
解答 解:(1)如图1中,
∵∠DCE=90°,∠DCF=60°,
∴∠BCE=30°,
∵AB⊥BC,
∴∠CBE=90°,
∴tan30°=$\frac{BE}{BC}$,
∴BE=$\frac{4\sqrt{3}}{3}$.
(2)如图2中,作DM⊥BC于M.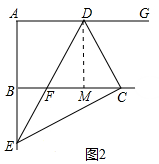
∵AG∥BC,AB⊥BC,
∴AG⊥AB,
∴∠A=∠ABM=∠DMB=90°,
∴四边形ABMD是矩形,
∴BM=AD=y,AB=DM=3,CM=4-y,
∵∠DCM+∠CDM=90°,∠DCM+∠BCE=90°,
∴∠CDM=∠BCE,∵∠DMC=∠CBE,
∴△DCM∽△CEB,
∴$\frac{DM}{CB}$=$\frac{CM}{EB}$,
∴$\frac{3}{4}$=$\frac{4-y}{x}$,
∴y=$\frac{3}{4}$x-4,(0≤x≤$\frac{16}{3}$).
(3)如图3中,
∵CD=CF,
∴∠CDF=∠CFD,
∵AG∥BC,
∴∠CFD=∠ADF,
∴∠EDA=∠EDC,
∵EA⊥DA,EC⊥DC,
∴EA=EC=x+3,
在Rt△BCE中,∵EC2=BE2+BC2,
∴(x+3)2=x2+42,
∴x=$\frac{7}{6}$,
∴BE=$\frac{7}{6}$.
点评 本题考查几何变换综合题、相似三角形的判定和性质、矩形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会正确寻找相似三角形解决问题,学会用方程的思想思考问题,属于中考压轴题.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两条边相等的两个直角三角形全等 | |
| B. | 等腰三角形顶角的平分线把它分成两个全等三角形 | |
| C. | 有一个角是60°的等腰三角形是等边三角形 | |
| D. | 底边相等的两个等腰直角三角形全等. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
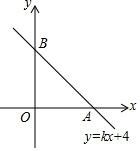 如图,在直角坐标系中,直线y=kx+4与x轴正半轴交于一点A,与y轴交于点B,已知△OAB的面积为10,求
如图,在直角坐标系中,直线y=kx+4与x轴正半轴交于一点A,与y轴交于点B,已知△OAB的面积为10,求查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 品名 | 黄瓜 | 茄子 |
| 批发价/(元/千克) | 2.4 | 2.2 |
| 零售价/(元/千克) | 3.6 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com