练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．（1）如图1，在正方形网格上有一个△ABC
    ①画△ABC关于直线MN的对称图形（不写作法）
    ②若网格上的每个小正方形的边长为1，求△ABC的面积．
    （2）在图2中作出△ABC的三条高AD，BE，CF．（不写作法） 

    分析 （1）①根据轴对称图形的画法，画出图形即可；②令AC与MN的交点为点D，利用分割图形求面积法即可求出△ABC的面积；
    （2）根据高线的画法，画出图形即可．

    解答 解：（1）①依照题意画出图形，如图1所示．

    ②令AC与MN的交点为点D，如图1所示．
    S△ABC=$\frac{1}{2}$×3×（4+2）=9．
    （2）依照题意画出图形，如图2所示．

    点评 本题考查了作图中的轴对称变换以及画三角形的高线，解题的关键是牢记轴对称图形以及三角形高线的画法．本题属于中档题，难度不大，解决该题型题目时，掌握各种图形变换的画法是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    9．如图，直线AB、CD相交于点O，OD平分∠BOF，OE⊥CD于O，若∠EOF=α，下列说法①∠AOC=α-90°；②∠EOB=180°-α；③∠AOF=360°-2α，其中正确的是（　　）
    A．①②B．①③C．②③D．①②③

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，四边形ABCD中任意一点P（x0，y0）经过平移后对应点为P1（x0+3，y0+3），将四边形ABCD作同样的平移得到四边形A1B1C1D1，求A1、B1、C1、D1的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，△ABO的顶点A、B、O均在格上，请你画出△ABO绕点O旋转180°后的△A1B1O．（不要求写作法、证明，但要在所画的三角形中标上顶点字母）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图每个小方格都是边长为1个单位的正方形，△ABC在平面直角坐标系的位置如图所示，先将△ABC向左平移4个单位，再向上平移2个单位，得到△A1B1C1
    （1）画出△ABC平移后的△A1B1C1；
    （3）写出A1、B1、C1的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

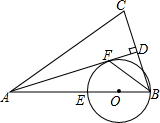    4．如图，在△ABC中，AB=AC，AD是BC边上的高线，BF平分∠ABC交AD于点F，以AB上的点O为圆心，OB为半径的⊙O交AB于点E，恰好经过点F．
    （1）求证：AD与⊙O相切；
    （2）当BC=4，AC=6时，求线段AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．两块等腰直角三角板ABC，DEF按图1的方式放置在同一条直线l上，点C与点F重合，线段EB绕点E逆时针旋转45°交AD于点M．已知∠ABC=∠DEF=90°，DE=2．
    （1）求证：AM=DM；
    （2）将图1中的三角板ABC沿直线l向左平移，如图2所示，设CE=x．
    ①求$\frac{AM}{DM}$的值（用含x的代数式表示）；
    ②若将图2中的三角板ABC绕点C逆时针旋转m°（0＜m＜45），原题中的其它条件保持不变，如图3所示，请探究：$\frac{AM}{DM}$的值是否发生变化，若有变化，请求出$\frac{AM}{DM}$的值（用含x的代数式表示）；若没有变化，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图1，在△ABC中，点D是BC的中点，延长AD到点G，使DG=AD，连接CG，可以得到△ABD≌△GCD，这种作辅助线的方法我们通常叫做“倍长中线法”．
    如图2，在△ABC中，点D是BC的中点，点E是AB上一点，连接ED，小明由图1中作辅助线的方法想到：延长ED到点G，使DG=ED，连接CG．
    （1）请直接写出线段BE和CG的关系：BE=CG；
    （2）如图3，若∠A=90°，过点D作DF⊥DE交AC于点F，连接EF，已知BE=3，CF=2$\sqrt{5}$，其它条件不变，求EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．若关于x的无理方程$\sqrt{{x}^{2}-p}$+2$\sqrt{{x}^{2}-1}$=x有实数解，求实数p的取值范围．

    查看答案和解析>>

    同步练习册答案