
 ��ͼ����֪˫����y1=$\frac{k}{x}$������D��6��1������C��˫���ߵ�������֧�ϵĶ��㣬����C��CA��x�ᣬ����D��BD��y�ᣬ����ֱ�ΪA��B������AB��BC��
��ͼ����֪˫����y1=$\frac{k}{x}$������D��6��1������C��˫���ߵ�������֧�ϵĶ��㣬����C��CA��x�ᣬ����D��BD��y�ᣬ����ֱ�ΪA��B������AB��BC������ ��1���ѵ�D���������˫���߽���ʽ�����м��㼴�ɵý⣻
��2�����ȸ��ݵ�D���������BD�ij��ȣ��ٸ��������ε������ʽ�����C��BD�ľ��룬Ȼ�������C�������꣬�ٴ��뷴������������ʽ�����C�����꣬Ȼ�����ô���ϵ������һ�κ�������ʽ���
�ڸ���ͼ�ɵõ�y1��y2ʱx��ȡֵ��Χ��
�۸������������A��B�����꣬Ȼ�����ô���ϵ���ɷ����ֱ��AB�Ľ���ʽ����֪��ֱ��CD�Ľ���ʽkֵ��ȣ�����AB��CDƽ�У�
��� �⣺��1����˫����y=$\frac{k}{x}$������D��6��1����
��$\frac{k}{6}$=1��
���k=6��
��2�������C��BD�ľ���Ϊh��
�ߵ�D������Ϊ��6��1����DB��y�ᣬ
��BD=6��
��S��BCD=$\frac{1}{2}$��6•h=12��
���h=4��
�ߵ�C��˫���ߵ��������ϵĶ��㣬��D��������Ϊ1��
���C��������Ϊ1-4=-3��
��$\frac{6}{x}$=-3��
���x=-2��
���C��������-2��-3����
��$\left\{\begin{array}{l}{-2a+b=-3}\\{6a+b=-2}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-2}\end{array}\right.$��
����ͼ��֪��x��-2��0��x��6ʱ��y1��y2��
��AB��CD��
�������£���CA��x�ᣬDB��y�ᣬ���C������Ϊ��c��$\frac{6}{c}$������D������Ϊ��6��1����
���A��B������ֱ�ΪA��c��0����B��0��1����
��ֱ��AB�Ľ���ʽΪy=mx+n��
��$\left\{\begin{array}{l}{mc+n=0}\\{n=1}\end{array}\right.$��
���$\left\{\begin{array}{l}{m=-\frac{1}{c}}\\{n=1}\end{array}\right.$��
���ԣ�ֱ��AB�Ľ���ʽΪy=-$\frac{1}{c}$x+1��
��ֱ��CD�Ľ���ʽΪy=ex+f��
��$\left\{\begin{array}{l}{ec+f=\frac{6}{c}}\\{6e+f=1}\end{array}\right.$��
���$\left\{\begin{array}{l}{e=-\frac{1}{c}}\\{f=\frac{c+6}{c}}\end{array}\right.$��
��ֱ��CD�Ľ���ʽΪy=-$\frac{1}{c}$x+$\frac{c+6}{c}$��
��AB��CD�Ľ���ʽk������-$\frac{1}{c}$��
��AB��CD��λ�ù�ϵ��AB��CD��
���� ���⿼����һ�κ����뷴���������Ľ������⣬��Ҫ�����˴���ϵ������������ʽ�������ε��������⣬����ϵ��������������ʽ��õķ�����һ��Ҫ�������ղ�������ã�


 �żӾ���ϵ�д�
�żӾ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{16}$ | B�� | $\sqrt{7}$ | C�� | $\frac{3}{11}$ | D�� | 3.14 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ֱ��a��b����A��ֱ��a�ϣ�AB��AC����ΪA������1=42�㣬���2Ϊ48�ȣ�
��ͼ��ֱ��a��b����A��ֱ��a�ϣ�AB��AC����ΪA������1=42�㣬���2Ϊ48�ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
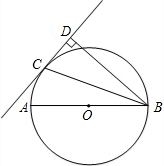 ��ͼ����C����ABΪֱ���ġ�O�ϵ�һ�㣬BD��CD������λ��D��BCƽ�֡�DBA��
��ͼ����C����ABΪֱ���ġ�O�ϵ�һ�㣬BD��CD������λ��D��BCƽ�֡�DBA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��5�� | B�� | ��-1��6�� | C�� | ��-1��-6�� | D�� | ��2��-3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��2 | B�� | x��2 | C�� | x��2 | D�� | x��2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com