
【题目】如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°,AE、AF分别交BD于M、N,连按EN、EF,有以下结论:
①△ABM∽△NEM;②△AEN是等腰直角三角形;③当AE=AF时,![]() ;④BE+DF=EF;⑤若点F是DC的中点,则CE
;④BE+DF=EF;⑤若点F是DC的中点,则CE![]() CB.
CB.
其中正确的个数是( )

A.2B.3C.4D.5
【答案】C
【解析】
①如图,证明△AMN∽△BME和△AMB∽△NME,
②利用相似三角形的性质可得∠NAE=∠AEN=45°,则△AEN是等腰直角三角形可作判断;
③先证明CE=CF,假设正方形边长为1,设CE=x,则BE=1-x,表示AC的长为AO+OC可作判断;
④如图3,将△ADF绕点A顺时针旋转90°得到△ABH,证明△AEF≌△AEH(SAS),则EF=EH=BE+BH=BE+DF,可作判断;
⑤如图4中,设正方形的边长为2a,则DF=CF=a,AF=![]() a,想办法求出BE,EC即可判断.
a,想办法求出BE,EC即可判断.
如图,∵四边形ABCD是正方形,
∴∠EBM=∠ADM=∠FDN=∠ABD=45°.
∵∠MAN=∠EBM=45°,∠AMN=∠BME,
∴△AMN∽△BME,
∴![]() ,
,
∴![]() ,
,
∵∠AMB=∠EMN,
∴△AMB∽△NME,故①正确,
∴∠AEN=∠ABD=45°,
∴∠NAE=∠AEN=45°,
∴△AEN是等腰直角三角形,故②正确,
在△ABE和△ADF中,
∵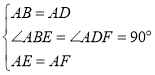 ,
,
∴Rt△ABE≌Rt△ADF(HL),∴BE=DF.
∵BC=CD,∴CE=CF,
假设正方形边长为1,设CE=x,则BE=1﹣x,
如图2,连接AC,交EF于H,
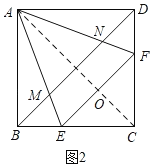
∵AE=AF,CE=CF,∴AC是EF的垂直平分线,
∴AC⊥EF,OE=OF,
Rt△CEF中,OC![]() EF
EF![]() x,
x,
在△EAF中,∠EAO=∠FAO=22.5°=∠BAE=22.5°,
∴OE=BE.
∵AE=AE,
∴Rt△ABE≌Rt△AOE(HL),
∴AO=AB=1,∴AC![]() AO+OC,
AO+OC,
∴1![]() x
x![]() ,
,
∴x=2![]() ,
,
∴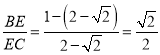 ,故③不正确,
,故③不正确,
③如图3,
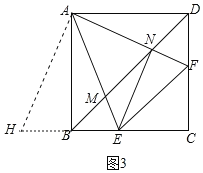
∴将△ADF绕点A顺时针旋转90°得到△ABH,
则AF=AH,∠DAF=∠BAH.
∵∠EAF=45°=∠DAF+∠BAE=∠HAE.
∵∠ABE=∠ABH=90°,
∴H、B、E三点共线,
在△AEF和△AEH中,
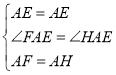 ,
,
∴△AEF≌△AEH(SAS),
∴EF=EH=BE+BH=BE+DF,故④正确,
如图4中,设正方形的边长为2a,则DF=CF=a,AF![]() a,
a,
∵DF∥AB,∴![]() ,
,
∴AN=NE![]() AF
AF![]() a,
a,
∴AE![]() AN
AN![]() a,
a,
∴BE![]() a,
a,
∴EC![]() a
a![]() BC,故⑤正确.
BC,故⑤正确.
故选:C.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
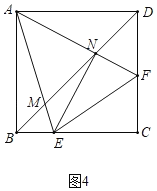
【题目】一列动车从甲地开往乙地, 一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为![]() (小时),两车之间的距离为
(小时),两车之间的距离为![]() (千米),如图中的折线表示
(千米),如图中的折线表示![]() 与
与![]() 之间的函数关系,下列说法:①动车的速度是
之间的函数关系,下列说法:①动车的速度是![]() 千米/小时;②点B的实际意义是两车出发后
千米/小时;②点B的实际意义是两车出发后![]() 小时相遇;③甲、乙两地相距
小时相遇;③甲、乙两地相距![]() 千米;④普通列车从乙地到达甲地时间是
千米;④普通列车从乙地到达甲地时间是![]() 小时,其中不正确的有( )
小时,其中不正确的有( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
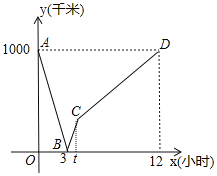
【题目】如图,抛物线![]() 经过点
经过点![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线上一个动点,设点
是抛物线上一个动点,设点![]() 的横坐标为
的横坐标为![]() .连接
.连接![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求抛物线的函数表达式;
(2)![]() 的面积何时最大?求出此时
的面积何时最大?求出此时![]() 点的坐标和最大面积;
点的坐标和最大面积;
(3)在(2)的条件下,若点![]() 是
是![]() 轴上一动点,点
轴上一动点,点![]() 是抛物线上一动点,试判断是否存在这样的点
是抛物线上一动点,试判断是否存在这样的点![]() ,使得以点
,使得以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形?若存在,请直接写出点
为顶点的四边形是平行四边形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为![]() ,四边形ABCD为⊙O的内接矩形,AD=6,M为DC中点,E为⊙O上的一个动点,连结DE,作DF⊥DE交射线EA于F,连结MF,则MF的最大值为_____.
,四边形ABCD为⊙O的内接矩形,AD=6,M为DC中点,E为⊙O上的一个动点,连结DE,作DF⊥DE交射线EA于F,连结MF,则MF的最大值为_____.
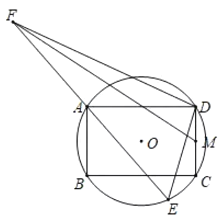
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解青少年形体情况,现随机抽查了某市若十名初中学生坐必、站姿.走安的好坏情况我们对测评数据作了适当处理(如果一个学生有一种以上:不良姿势.以他最突出的一种作记载) ,并将统计结果绘制了如下两幅不完整的统计图.请你根据图中所给信息解答下列问题:
![]() 求这次抽查一共抽查了多少名学生;
求这次抽查一共抽查了多少名学生;
![]() 请将条形统计图补充完整;
请将条形统计图补充完整;
![]() 如果全市有
如果全市有![]() 万名初中生,那么全市初中生中,三姿良好的学生约有多少名
万名初中生,那么全市初中生中,三姿良好的学生约有多少名

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.
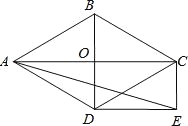
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2![]() 时,求sin∠AED的值,求∠EAD的正切值.
时,求sin∠AED的值,求∠EAD的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() (x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB丄x轴于点B,点A与点B关于y轴对称.
(x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB丄x轴于点B,点A与点B关于y轴对称.

(1)求一次函数、反比例函数的解析式;
(2)求证:点C为线段AP的中点;
(3)反比例函数图象上是否存在点D,使四边形BCPD为菱形,如果存在,说明理由并求出点D的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,m),且与x铀的一个交点在点(3,0)和(4,0)之间,则下列结论:①abc>0;②a﹣b+c>0;③b2=4a(c﹣m);④一元二次方程ax2+bx+c=m+1有两个不相等的实数根,其中正确结论的个数是( )

A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com