
【题目】如图,四边形ABCD为菱形,E为对角线AC上的一个动点,连结DE并延长交射线AB于点F,连结BE.
(1)求证:∠AFD=∠EBC;
(2)若∠DAB=90°,当△BEF为等腰三角形时,求∠EFB的度数.
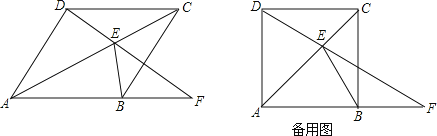
【答案】(1)见解析;(2) ∠EFB=30°或120°.
【解析】
(1)直接利用全等三角形的判定方法得出△DCE≌△BCE(SAS),即可得出答案;
(2)利用正方形的性质结合等腰三角形的性质得出:①当F在AB延长线上时;②当F在线段AB上时;分别求出即可.
(1)证明:∵四边形ABCD是菱形,
∴CD=AB,∠ACD=∠ACB,
在△DCE和△BCE中
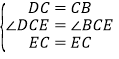 ,
,
∴△DCE≌△BCE(SAS),
∴∠CDE=∠CBE,
∵CD∥AB,
∴∠CDE=∠AFD,
∴∠EBC=∠AFD.
(2)分两种情况,
①如图1,当F在AB延长线上时,
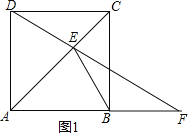
∵∠EBF为钝角,
∴只能是BE=BF,设∠BEF=∠BFE=x°,
可通过三角形内角形为180°得:90+x+x+x=180,
解得:x=30,
∴∠EFB=30°.
②如图2,当F在线段AB上时,
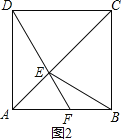
∵∠EFB为钝角,
∴只能是FE=FB,设∠BEF=∠EBF=x°,则有∠AFD=2x°,
可证得:∠AFD=∠FDC=∠CBE,
得x+2x=90,
解得:x=30,
∴∠EFB=120°.
综上:∠EFB=30°或120°.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
【题目】厦深铁路开通后,直线l1与l2分别表示从深圳北开往潮阳站的动车和从潮阳站开往深圳的高铁,两车同时出发,设动车离深圳北的距离为y1(千米),高铁离深圳的距离为距离y2(千米),行驶时间为t(小时),与t的函数关系如图所示:
(1)高铁的速度为 km/h;
(2)动车的速度为 km/h;
(3)动车出发多少小时与高铁相遇?
(4)两车出发经过多长时间相距50千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.为了了解全国中学生每天体育锻炼的时间,应采用普查的方式
B.若甲组数据的方差s ![]() =0.03,乙组数据的方差是s
=0.03,乙组数据的方差是s ![]() =0.2,则乙组数据比甲组数据稳定
=0.2,则乙组数据比甲组数据稳定
C.广安市明天一定会下雨
D.一组数据4、5、6、5、2、8的众数是5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店今年1月份购进一批笔记本,共2290本,每本进价为10元,该文具店决定从2月份开始进行销售,若每本售价为11元,则可全部售出;且每本售价每增长0.5元,销量就减少15本.
(1)若该种笔记本在2月份的销售量不低于2200本,则2月份售价应不高于多少元?
(2)由于生产商提高造纸工艺,该笔记本的进价提高了10%,文具店为了增加笔记本的销量,进行了销售调整,售价比中2月份在(1)的条件下的最高售价减少了 ![]() m%,结果3月份的销量比2月份在(1)的条件下的最低销量增加了m%,3月份的销售利润达到6600元,求m的值.
m%,结果3月份的销量比2月份在(1)的条件下的最低销量增加了m%,3月份的销售利润达到6600元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由甲、乙两个工程队承包某校校园绿化工程,甲、乙两队单独完成这项工程所需时间比是3︰2,两队合做6天可以完成.
(1)求两队单独完成此项工程各需多少天?
(2)此项工程由甲、乙两队合做6天完成任务后,学校付给他们20000元报酬,若
按各自完成的工程量分配这笔钱,问甲、乙两队各得到多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级两个班,各选派10名学生参加学校举行的“数学奥林匹克”大赛预赛,各参赛选手的成绩如下:
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
九(1)班 | 100 | 94 | b | 93 | 12 |
九(2)班 | 99 | a | 95.5 | 93 | 8.4 |
(1)直接写出表中a、b的值:a= , b=;
(2)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,求另外两个决赛名额落在不同班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,G为⊙O上一点,AG交CD于K,E为CD延长线上一点,且EK=EG,EG的延长线交AB的延长线于F. 
(1)求证:EF为⊙O的切线;
(2)若DK=2HK=AK,CH= ![]() ,求图中阴影部分的面积S.
,求图中阴影部分的面积S.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,
上,![]() 射线
射线![]() 绕
绕![]() 点顺时针旋转至
点顺时针旋转至![]() 便立即逆时针回转,射线
便立即逆时针回转,射线![]() 绕
绕![]() 点顺时针旋转至
点顺时针旋转至![]() 便立即逆时针回转.射线
便立即逆时针回转.射线![]() 转动的速度是每秒
转动的速度是每秒![]() 度,射线
度,射线![]() 转动的速度是每秒
转动的速度是每秒![]() 度.
度.

(1)直接写出![]() 的大小为_______;
的大小为_______;
(2)射线![]() 、
、![]() 转动后对应的射线分别为
转动后对应的射线分别为![]() 、
、![]() ,射线
,射线![]() 交直线
交直线![]() 于点
于点![]() ,若射线
,若射线![]() 比射线
比射线![]() 先转动
先转动![]() 秒,设射线
秒,设射线![]() 转动的时间为
转动的时间为![]()
![]() 秒,求
秒,求![]() 为多少时,直线
为多少时,直线![]() 直线
直线![]() ?
?
(3)如图2,若射线![]() 、
、![]() 同时转动
同时转动![]()
![]() 秒,转动的两条射线交于点
秒,转动的两条射线交于点![]() ,作
,作![]() ,点
,点![]() 在
在![]() 上,请探究
上,请探究![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
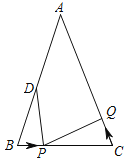
【题目】如图,已知△ABC中,AB=AC=12cm,∠B=∠C,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以2cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,则经过多少秒后,点P与点Q第一次在△ABC的哪条边上相遇?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com