
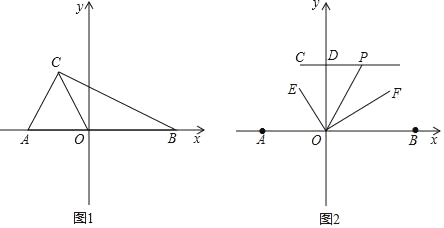
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�A��m��0����B��n��0����C����1��2����������ʽ|m+2|+��m+n��2��2��0��
��1�����m��n��ֵ��
��2������x����������ϴ���һ��M��ʹ��COM�����������ABC�������һ�룬�����M�����ꣻ
���������������λ���Ƿ���ڵ�M��ʹ��COM�����������ABC�������һ����Ȼ�����������ڣ���ֱ���������ĺ�����д�����������ĵ�M�����ꣻ
��3����ͼ2������C��CD��y�ύy���ڵ�D����PΪ�߶�CD�ӳ�����һ���㣬����OP��OEƽ�֡�AOP��OF��OE������P�˶�ʱ��![]() ��ֵ�Ƿ��ı䣿�����䣬����ֵ�����ı䣬˵�����ɣ�
��ֵ�Ƿ��ı䣿�����䣬����ֵ�����ı䣬˵�����ɣ�
���𰸡���1��m=��2��n=4����2����M������Ϊ��3��0�����ڵ�M������Ϊ��3��0����3��0����0��6����0����6������3��2��
��������
��1�����ݷǸ����������г������飬�ⷽ���鼴�ɣ�
��2���ٸ��������ε������ʽ���㼴�ɣ�
�ڷֵ�M��x��y��������������㣻
��3�����ݽ�ƽ���ߵĶ��塢��ֱ�Ķ���õ���POF=��BOF�����POF=��BOF=x����DOE=y�����ͼ�εõ�x=y���õ��𰸣�
��1��������ã�![]() ����ã�
����ã�![]() ����m=��2��n=4��
����m=��2��n=4��
��2�������M�����������Ϊ��x��0������ABC�����![]() 6��2=6��������ã�
6��2=6��������ã�![]() x��2
x��2![]() 6����ã�x=3����COM��������ڡ�ABC�������һ��ʱ����M������Ϊ��3��0����
6����ã�x=3����COM��������ڡ�ABC�������һ��ʱ����M������Ϊ��3��0����
�ڵ���M��x����ʱ���ɢٵã���M������Ϊ��3��0����3��0��������M��y����ʱ�����M�����������Ϊ��0��y����������ã�![]() |y|��1
|y|��1![]() 6����ã�y=��6��
6����ã�y=��6��
�������������������ĵ�M������Ϊ��3��0����3��0����0��6����0����6����
��3��![]() 2������ı䣮
2������ı䣮
��OEƽ�֡�AOP�����EOP=��AOE��
��OF��OE�����EOP+��POF=90�㣬��AOE+��BOF=90�㣬���POF=��BOF�����POF=��BOF=x����DOE=y��
��CD��y�ᣬ��CD��x�ᣬ���OPD=��POB=2x�����POD=90�㩁2x��
�ߡ�EOF=90�㣬��y+90�㩁2x+x=90�㣬��ã�x=y�����OPD=2��DOE����![]() 2��
2��


 �¿α�ͬ��ѵ��ϵ�д�
�¿α�ͬ��ѵ��ϵ�д� һ����ʦ����Ӧ����������һ��ȫϵ�д�
һ����ʦ����Ӧ����������һ��ȫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
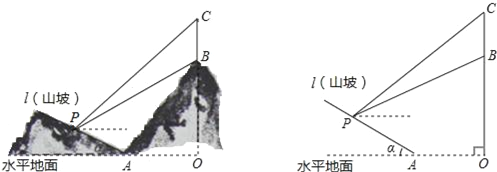
����Ŀ����ͼ��ʾ��ij���̶�����ɽ�£�ɽ����Ϊֱ��l������һ��·����Ҫ����ɽ�µ��¶ȣ���tan����ֵ������Ա��ɽ��P�������ƴ������ߣ��۲����ɽ���ϵ�һ���������������C������Ϊ31�㣬����B������Ϊ26.6�㣮��֪����BC=40�ף������ڵ�ɽ��OB=240�ף�OA=300�ף�ͼ�еĵ�O��B��C��A��P��ͬһƽ���ڣ�
��
��1��P��OC�ľ��룮
��2��ɽ�µ��¶�tan����
�������sin26.6���0.45��tan26.6���0.50��sin31���0.52��tan31���0.60��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ABCD���ܳ�Ϊ12��E��F��G��HΪ����ABCD�ĸ����е�����AB��x���ı���EFGH�����Ϊy.
(1)��ֱ��д��y��x֮��ĺ�����ϵʽ��
(2)����(1)�еĺ�����ϵʽ�����㵱xΪ��ֵʱ��y�������������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD���ĸ�����������ǡ��ƴ��һ����϶���ص����ı���EFGH��EH=12���ף�EF=16���ף����AD�ij��ǣ�������

A. 12���� B. 16���� C. 20���� D. 28����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
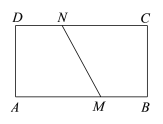
����Ŀ����ͼ��һ�ž���ֽƬABCD��AD��9 cm��AB��12 cm����ֽƬ�۵�ʹA��C�����غϣ���ô�ۺ�MN��________cm.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P���߶�AB���е㣬QΪ�߶�PB��һ�㣬�ֱ���AQ��AP��PQ��QBΪһ���������Σ��������Ӧ�ؼ���SACDQ��SAEFP��SPGHQ��SQIJB����AP��m��QB��n��
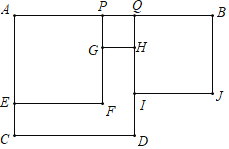
��1���ú���m��n�Ĵ���ʽ��ʾ������ACDQ�����SACDQ��
��2��SACDQ+SQIJB��SAEFP+SPGHQ����������������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�غ�����A�ӵ�̨�羯�����ڸó������Ϸ���260 km��B����һ̨�����ģ���BC������15 km/h���ٶ���C�ƶ�����֪����A��BC�ľ���AD��100 km����ǫ̂�����ľ����ʱ���B���ƶ���D�㣿����ھ�̨������30 km��Բ�������ڶ����ܵ�̨���Ӱ�죬����D����Ϣ�������ڽӵ�̨�羯����ļ�Сʱ�ڳ���ſ�������̨���Ӱ�죿

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCΪ����ֱ�������Σ���BCA��90����AC��BC����M��N��б��AB�ϣ��ҡ�MCN��45������̽���߶�AM,��MN��BN֮��Ĺ�ϵ����˵�����ɡ�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����߳�Ϊ3�ĵȱ�������ABC�ı�AB��һ��P����PE��AC��E��QΪBC�ӳ�����һ�㣬�ʣ���PA��CQʱ������PQ��AC����D����DE�ij���

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com