
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数m | 58 | 96 | 116 | 295 | 484 | 601 |
| 摸到白球的频率$\frac{m}{n}$ | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
分析 (1)根据利用频率估计概率,由于摸到白球的频率稳定在0.6左右,由此可估计摸到白球的概率为0.6;
(2)根据(1)可得摸到白球的概率是0.6,再用1减去白球的概率,即可得出黑球的概率;
(3)用总的个数乘以摸到黑球的概率,即可得出答案.
解答 解:(1)根据摸到白球的频率稳定在0.6左右,
所以摸到白球的频率将会接近0.6;
(2)由(1)可得:摸到白球的概率为0.6;摸到黑球的概率是1-0.6=0.4;
故答案为:0.6,0.4;
(3)由(2)可得:
20×0.4=8(个),
答:黑球有8只.
点评 此题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率;用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:选择题
| A. | 图象在第一、三象限 | B. | 图象经过点(2,-8) | ||
| C. | 当x>0时,y随x的增大而减小 | D. | 当x<0时,y随x的增大而增大 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
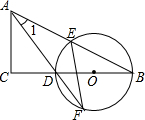 如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连结EF.
如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连结EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
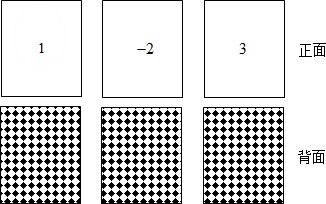
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
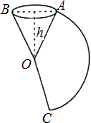 如图,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12cm,OA=13cm,则扇形AOC中$\widehat{AC}$的长是10πcm(计算结果保留π).
如图,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12cm,OA=13cm,则扇形AOC中$\widehat{AC}$的长是10πcm(计算结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
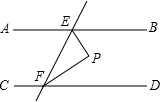 如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=44°,则∠EPF=67°.
如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=44°,则∠EPF=67°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com